Was ist lineare Regression beim maschinellen Lernen?

Die lineare Regression ist eine grundlegende Technik in der Datenanalyse und im maschinellen Lernen (ML). Dieser Leitfaden hilft Ihnen, die lineare Regression, ihren Aufbau sowie ihre Arten, Anwendungen, Vor- und Nachteile zu verstehen.

Inhaltsverzeichnis

• Was ist lineare Regression?
• Arten der linearen Regression
• Lineare Regression vs. logistische Regression
• Wie funktioniert die lineare Regression?
• Anwendungen der linearen Regression
• Vorteile der linearen Regression in ML
• Nachteile der linearen Regression in ML

Was ist lineare Regression?

Die lineare Regression ist eine statistische Methode, die beim maschinellen Lernen verwendet wird, um die Beziehung zwischen einer abhängigen Variablen und einer oder mehreren unabhängigen Variablen zu modellieren. Es modelliert Beziehungen, indem es eine lineare Gleichung an beobachtete Daten anpasst, dient oft als Ausgangspunkt für komplexere Algorithmen und wird häufig in der Vorhersageanalyse verwendet.

Im Wesentlichen modelliert die lineare Regression die Beziehung zwischen einer abhängigen Variablen (dem Ergebnis, das Sie vorhersagen möchten) und einer oder mehreren unabhängigen Variablen (den Eingabemerkmalen, die Sie für die Vorhersage verwenden), indem die am besten passende gerade Linie durch eine Reihe von Datenpunkten ermittelt wird. Diese Linie,Regressionsliniegenannt, stellt die Beziehung zwischen der abhängigen Variablen (dem Ergebnis, das wir vorhersagen möchten) und der/den unabhängigen Variablen (den Eingabemerkmalen, die wir für die Vorhersage verwenden) dar. Die Gleichung für eine einfache lineare Regressionsgerade ist definiert als:

y = mx + c

Dabei ist y die abhängige Variable, x die unabhängige Variable, m die Steigung der Geraden und c der y-Achsenabschnitt. Diese Gleichung stellt ein mathematisches Modell für die Zuordnung von Eingaben zu vorhergesagten Ausgaben bereit, mit dem Ziel, die Unterschiede zwischen vorhergesagten und beobachteten Werten, die als Residuen bezeichnet werden, zu minimieren. Durch die Minimierung dieser Residuen erzeugt die lineare Regression ein Modell, das die Daten am besten darstellt.

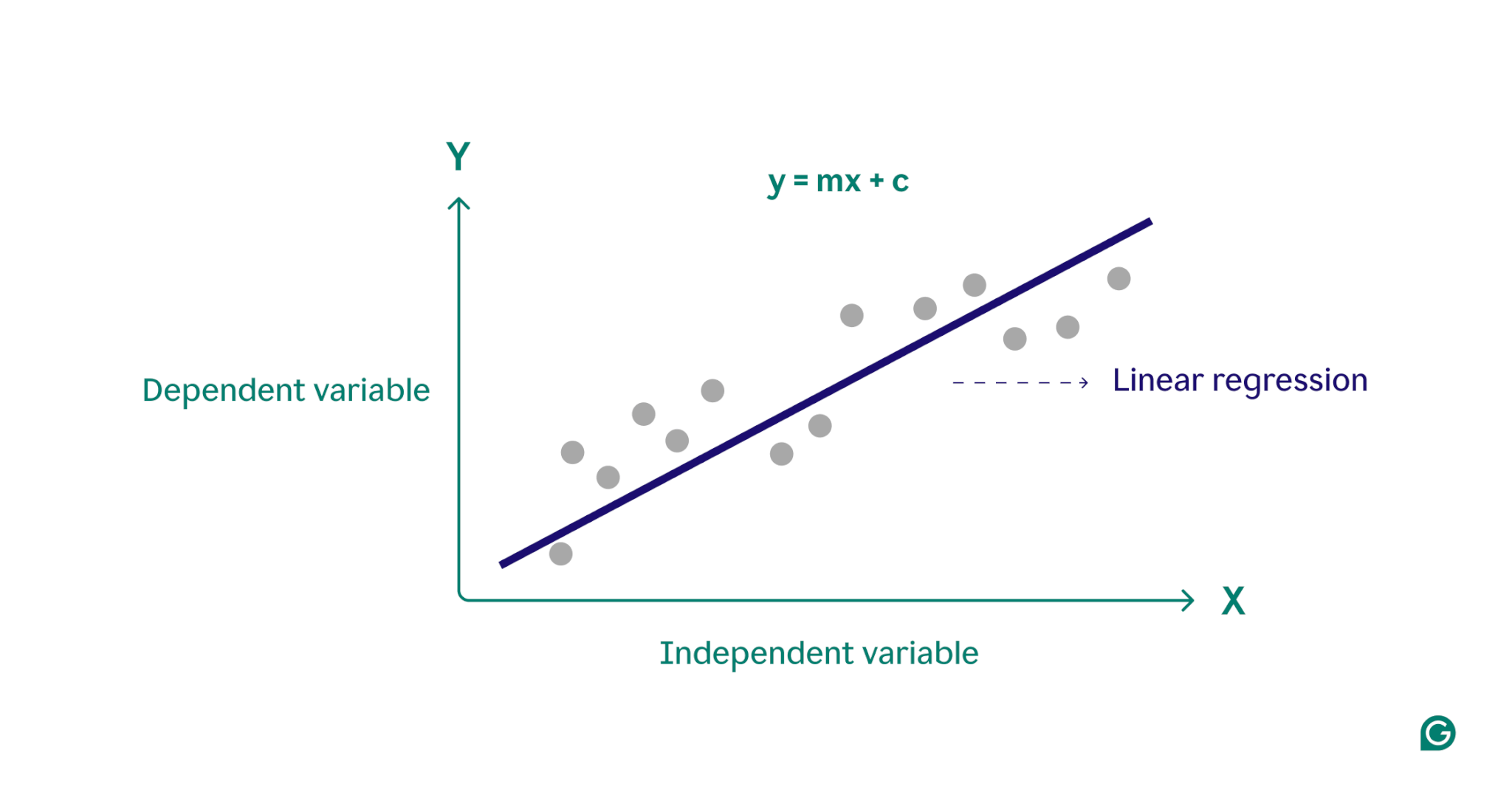
Konzeptionell kann man sich die lineare Regression als das Zeichnen einer geraden Linie durch Punkte in einem Diagramm vorstellen, um festzustellen, ob zwischen diesen Datenpunkten eine Beziehung besteht. Das ideale lineare Regressionsmodell für eine Reihe von Datenpunkten ist die Linie, die die Werte aller Punkte im Datensatz am besten annähert.

Arten der linearen Regression

Es gibt zwei Haupttypen der linearen Regression:einfache lineare Regressionundmultiple lineare Regression.

Einfache lineare Regression

Die einfache lineare Regression modelliert die Beziehung zwischen einer einzelnen unabhängigen Variablen und einer abhängigen Variablen mithilfe einer geraden Linie. Die Gleichung für die einfache lineare Regression lautet:

y = mx + c

Dabei ist y die abhängige Variable, x die unabhängige Variable, m die Steigung der Geraden und c der y-Achsenabschnitt.

Diese Methode ist eine einfache Möglichkeit, klare Erkenntnisse bei der Bearbeitung von Szenarien mit einer Variablen zu gewinnen. Stellen Sie sich einen Arzt vor, der herausfinden möchte, wie sich die Körpergröße des Patienten auf das Gewicht auswirkt. Durch die Darstellung jeder Variablen in einem Diagramm und das Finden der am besten passenden Linie mithilfe einer einfachen linearen Regression konnte der Arzt das Gewicht eines Patienten allein anhand seiner Körpergröße vorhersagen.

Multiple lineare Regression

Die multiple lineare Regression erweitert das Konzept der einfachen linearen Regression um mehr als eine Variable und ermöglicht die Analyse, wie sich mehrere Faktoren auf die abhängige Variable auswirken. Die Gleichung für die multiple lineare Regression lautet:

y = b ₀ + b ₁ x ₁ + b ₂ x ₂ + … + b _n x _n

Dabei ist y die abhängige Variable, x ₁ , x ₂ , …, x _n sind die unabhängigen Variablen und b ₁ , b ₂ , …, b _n sind die Koeffizienten, die die Beziehung zwischen jeder unabhängigen Variablen und der abhängigen Variablen beschreiben.

Betrachten Sie als Beispiel einen Immobilienmakler, der die Immobilienpreise schätzen möchte. Der Agent könnte eine einfache lineare Regression verwenden, die auf einer einzelnen Variablen wie der Größe des Hauses oder der Postleitzahl basiert. Dieses Modell wäre jedoch zu einfach, da die Immobilienpreise häufig durch ein komplexes Zusammenspiel mehrerer Faktoren bestimmt werden. Eine multiple lineare Regression, die Variablen wie die Größe des Hauses, die Nachbarschaft und die Anzahl der Schlafzimmer einbezieht, wird wahrscheinlich ein genaueres Vorhersagemodell liefern.

Lineare Regression vs. logistische Regression

Lineare Regression wird oft mit logistischer Regression verwechselt. Während die lineare Regression Ergebnisse fürkontinuierlicheVariablen vorhersagt, wird die logistische Regression verwendet, wenn die abhängige Variablekategorial, oft binär (ja oder nein) ist. Kategoriale Variablen definieren nicht numerische Gruppen mit einer endlichen Anzahl von Kategorien, wie etwa Altersgruppe oder Zahlungsmethode. Kontinuierliche Variablen hingegen können jeden numerischen Wert annehmen und sind messbar. Beispiele für kontinuierliche Variablen sind Gewicht, Preis und Tagestemperatur.

Im Gegensatz zur linearen Funktion, die bei der linearen Regression verwendet wird, modelliert die logistische Regression die Wahrscheinlichkeit eines kategorialen Ergebnisses mithilfe einer S-förmigen Kurve, die als logistische Funktion bezeichnet wird. Im Beispiel der binären Klassifizierung fallen Datenpunkte, die zur Kategorie „Ja“ gehören, auf eine Seite der S-Form, während die Datenpunkte in der Kategorie „Nein“ auf die andere Seite fallen. Praktisch gesehen kann die logistische Regression verwendet werden, um zu klassifizieren, ob es sich bei einer E-Mail um Spam handelt oder nicht, oder um vorherzusagen, ob ein Kunde ein Produkt kaufen wird oder nicht. Im Wesentlichen wird die lineare Regression zur Vorhersage quantitativer Werte verwendet, während die logistische Regression für Klassifizierungsaufgaben verwendet wird.

Wie funktioniert die lineare Regression?

Bei der linearen Regression wird die am besten passende Gerade durch eine Reihe von Datenpunkten ermittelt. Dieser Prozess umfasst:

1 Auswahl des Modells:Im ersten Schritt wird die geeignete lineare Gleichung zur Beschreibung des Zusammenhangs zwischen den abhängigen und unabhängigen Variablen ausgewählt.

2 Anpassen des Modells:Als Nächstes wird eine Technik namens Ordinary Least Squares (OLS) verwendet, um die Summe der quadrierten Differenzen zwischen den beobachteten Werten und den vom Modell vorhergesagten Werten zu minimieren. Dies geschieht durch Anpassen der Steigung und des Achsenabschnitts der Linie, um die beste Anpassung zu finden. Der Zweck dieser Methode besteht darin, den Fehler oder die Differenz zwischen den vorhergesagten und den tatsächlichen Werten zu minimieren. Dieser Anpassungsprozess ist ein zentraler Bestandteil des überwachten maschinellen Lernens, bei dem das Modell aus den Trainingsdaten lernt.

3 Bewertung des Modells:Im letzten Schritt wird die Qualität der Anpassung mithilfe von Metriken wie dem R-Quadrat bewertet, das den Anteil der Varianz in der abhängigen Variablen misst, der aus den unabhängigen Variablen vorhersagbar ist. Mit anderen Worten: Das R-Quadrat misst, wie gut die Daten tatsächlich zum Regressionsmodell passen.

Dieser Prozess generiert ein maschinelles Lernmodell, mit dem dann Vorhersagen auf der Grundlage neuer Daten getroffen werden können.

Anwendungen der linearen Regression in ML

Beim maschinellen Lernen ist die lineare Regression ein häufig verwendetes Werkzeug zur Vorhersage von Ergebnissen und zum Verständnis der Beziehungen zwischen Variablen in verschiedenen Bereichen. Hier sind einige bemerkenswerte Beispiele seiner Anwendungen:

Prognose der Verbraucherausgaben

Einkommensniveaus können in einem linearen Regressionsmodell verwendet werden, um Verbraucherausgaben vorherzusagen. Insbesondere könnte die multiple lineare Regression Faktoren wie historisches Einkommen, Alter und Beschäftigungsstatus einbeziehen, um eine umfassende Analyse zu ermöglichen. Dies kann Ökonomen bei der Entwicklung datengesteuerter Wirtschaftspolitiken unterstützen und Unternehmen dabei helfen, die Verhaltensmuster der Verbraucher besser zu verstehen.

Analyse der Marketingwirkung

Vermarkter können die lineare Regression nutzen, um zu verstehen, wie sich Werbeausgaben auf den Umsatz auswirken. Durch die Anwendung eines linearen Regressionsmodells auf historische Daten können zukünftige Verkaufserlöse vorhergesagt werden, sodass Vermarkter ihre Budgets und Werbestrategien für maximale Wirkung optimieren können.

Aktienkurse vorhersagen

In der Finanzwelt ist die lineare Regression eine der vielen Methoden zur Vorhersage von Aktienkursen. Anhand historischer Aktiendaten und verschiedener Wirtschaftsindikatoren können Analysten und Investoren mehrere lineare Regressionsmodelle erstellen, die ihnen dabei helfen, intelligentere Anlageentscheidungen zu treffen.

Vorhersage von Umweltbedingungen

In den Umweltwissenschaften kann die lineare Regression zur Vorhersage von Umweltbedingungen verwendet werden. Beispielsweise können verschiedene Faktoren wie Verkehrsaufkommen, Wetterbedingungen und Bevölkerungsdichte dabei helfen, Schadstoffwerte vorherzusagen. Diese Modelle des maschinellen Lernens können dann von politischen Entscheidungsträgern, Wissenschaftlern und anderen Interessengruppen verwendet werden, um die Auswirkungen verschiedener Maßnahmen auf die Umwelt zu verstehen und abzumildern.

Vorteile der linearen Regression in ML

Die lineare Regression bietet mehrere Vorteile, die sie zu einer Schlüsseltechnik beim maschinellen Lernen machen.

Einfach zu bedienen und umzusetzen

Im Vergleich zu den meisten mathematischen Werkzeugen und Modellen ist die lineare Regression leicht zu verstehen und anzuwenden. Es eignet sich besonders gut als Ausgangspunkt für neue Praktiker des maschinellen Lernens und bietet wertvolle Erkenntnisse und Erfahrungen als Grundlage für fortgeschrittenere Algorithmen.

Rechnerisch effizient

Modelle für maschinelles Lernen können ressourcenintensiv sein. Die lineare Regression erfordert im Vergleich zu vielen Algorithmen eine relativ geringe Rechenleistung und kann dennoch aussagekräftige prädiktive Erkenntnisse liefern.

Interpretierbare Ergebnisse

Fortgeschrittene statistische Modelle sind zwar leistungsstark, aber oft schwer zu interpretieren. Mit einem einfachen Modell wie der linearen Regression ist die Beziehung zwischen Variablen leicht zu verstehen und die Auswirkung jeder Variablen wird durch ihren Koeffizienten klar angezeigt.

Grundlage für fortgeschrittene Techniken

Das Verständnis und die Implementierung der linearen Regression bieten eine solide Grundlage für die Erforschung fortgeschrittenerer Methoden des maschinellen Lernens. Beispielsweise baut die polynomiale Regression auf der linearen Regression auf, um komplexere, nichtlineare Beziehungen zwischen Variablen zu beschreiben.

Nachteile der linearen Regression in ML

Obwohl die lineare Regression ein wertvolles Werkzeug beim maschinellen Lernen ist, weist sie einige bemerkenswerte Einschränkungen auf. Das Verständnis dieser Nachteile ist entscheidend für die Auswahl des geeigneten Tools für maschinelles Lernen.

Annahme eines linearen Zusammenhangs

Das lineare Regressionsmodell geht davon aus, dass die Beziehung zwischen abhängigen und unabhängigen Variablen linear ist. In komplexen realen Szenarien ist dies möglicherweise nicht immer der Fall. Beispielsweise ist die Körpergröße eines Menschen im Laufe seines Lebens nichtlinear, wobei sich das schnelle Wachstum in der Kindheit verlangsamt und im Erwachsenenalter aufhört. Daher könnte die Vorhersage der Höhe mithilfe der linearen Regression zu ungenauen Vorhersagen führen.

Empfindlichkeit gegenüber Ausreißern

Ausreißer sind Datenpunkte, die deutlich von den meisten Beobachtungen in einem Datensatz abweichen. Bei unsachgemäßer Handhabung können diese Extremwertpunkte die Ergebnisse verzerren und zu ungenauen Schlussfolgerungen führen. Beim maschinellen Lernen bedeutet diese Empfindlichkeit, dass Ausreißer die Vorhersagegenauigkeit und Zuverlässigkeit des Modells unverhältnismäßig beeinträchtigen können.

Multikollinearität

In mehreren linearen Regressionsmodellen können stark korrelierte unabhängige Variablen die Ergebnisse verzerren, ein Phänomen, das alsMultikollinearitätbekannt ist. Beispielsweise besteht möglicherweise ein enger Zusammenhang zwischen der Anzahl der Schlafzimmer in einem Haus und seiner Größe, da größere Häuser tendenziell über mehr Schlafzimmer verfügen. Dies kann es schwierig machen, den individuellen Einfluss einzelner Variablen auf die Immobilienpreise zu bestimmen, was zu unzuverlässigen Ergebnissen führt.

Annahme einer konstanten Fehlerstreuung

Bei der linearen Regression wird davon ausgegangen, dass die Unterschiede zwischen den beobachteten und den vorhergesagten Werten (die Fehlerstreuung) für alle unabhängigen Variablen gleich sind. Wenn dies nicht der Fall ist, sind die vom Modell generierten Vorhersagen möglicherweise unzuverlässig. Beim überwachten maschinellen Lernen kann das Versäumnis, die Fehlerstreuung zu berücksichtigen, dazu führen, dass das Modell voreingenommene und ineffiziente Schätzungen generiert, was seine Gesamteffektivität verringert.