¿Qué es la regresión lineal en el aprendizaje automático?
Publicado: 2024-09-06La regresión lineal es una técnica fundamental en el análisis de datos y el aprendizaje automático (ML). Esta guía le ayudará a comprender la regresión lineal, cómo se construye y sus tipos, aplicaciones, beneficios y desventajas.
Tabla de contenido
- ¿Qué es la regresión lineal?
- Tipos de regresión lineal
- Regresión lineal versus regresión logística
- ¿Cómo funciona la regresión lineal?
- Aplicaciones de la regresión lineal
- Ventajas de la regresión lineal en ML
- Desventajas de la regresión lineal en ML
¿Qué es la regresión lineal?
La regresión lineal es un método estadístico utilizado en el aprendizaje automático para modelar la relación entre una variable dependiente y una o más variables independientes. Modela relaciones ajustando una ecuación lineal a los datos observados, lo que a menudo sirve como punto de partida para algoritmos más complejos y se usa ampliamente en análisis predictivos.
Básicamente, la regresión lineal modela la relación entre una variable dependiente (el resultado que desea predecir) y una o más variables independientes (las características de entrada que utiliza para la predicción) al encontrar la línea recta que mejor se ajusta a través de un conjunto de puntos de datos. Esta línea, llamadalínea de regresión, representa la relación entre la variable dependiente (el resultado que queremos predecir) y las variables independientes (las características de entrada que utilizamos para la predicción). La ecuación para una recta de regresión lineal simple se define como:
y = mx + c
donde y es la variable dependiente, x es la variable independiente, m es la pendiente de la recta y c es la intersección con el eje y. Esta ecuación proporciona un modelo matemático para mapear entradas y salidas predichas, con el objetivo de minimizar las diferencias entre los valores predichos y observados, conocidos como residuos. Al minimizar estos residuos, la regresión lineal produce un modelo que representa mejor los datos.
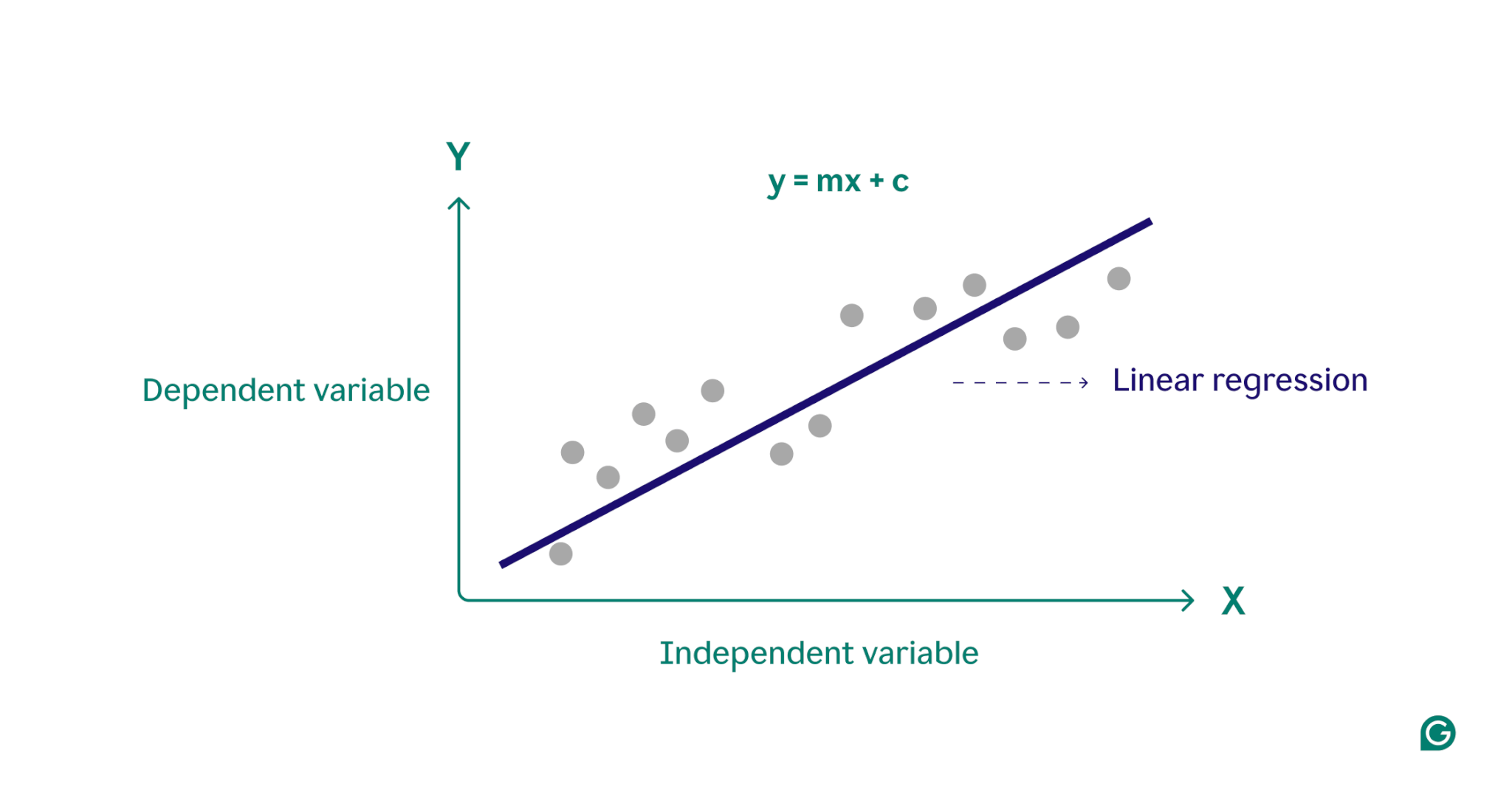
Conceptualmente, la regresión lineal se puede visualizar como dibujar una línea recta a través de puntos en un gráfico para determinar si existe una relación entre esos puntos de datos. El modelo de regresión lineal ideal para un conjunto de puntos de datos es la línea que mejor se aproxima a los valores de cada punto del conjunto de datos.
Tipos de regresión lineal
Hay dos tipos principales de regresión lineal:regresión lineal simpleyregresión lineal múltiple.
Regresión lineal simple
La regresión lineal simple modela la relación entre una única variable independiente y una variable dependiente utilizando una línea recta. La ecuación de regresión lineal simple es:
y = mx + c
donde y es la variable dependiente, x es la variable independiente, m es la pendiente de la recta y c es la intersección con el eje y.
Este método es una forma sencilla de obtener información clara cuando se trata de escenarios de una sola variable. Considere un médico que intenta comprender cómo la altura del paciente afecta el peso. Al trazar cada variable en un gráfico y encontrar la línea que mejor se ajusta mediante una regresión lineal simple, el médico podría predecir el peso de un paciente basándose únicamente en su altura.
Regresión lineal múltiple
La regresión lineal múltiple amplía el concepto de regresión lineal simple para dar cabida a más de una variable, lo que permite el análisis de cómo múltiples factores impactan la variable dependiente. La ecuación para la regresión lineal múltiple es:
y = b 0 + b 1 x 1 + b 2 x 2 + … + b n x n
donde y es la variable dependiente, x 1 , x 2 ,…, x n son las variables independientes, y b 1 , b 2 ,…, b n son los coeficientes que describen la relación entre cada variable independiente y la variable dependiente.
Como ejemplo, consideremos un agente de bienes raíces que quiere estimar los precios de una vivienda. El agente podría usar una regresión lineal simple basada en una sola variable, como el tamaño de la casa o el código postal, pero este modelo sería demasiado simplista, ya que los precios de la vivienda a menudo dependen de una interacción compleja de múltiples factores. Una regresión lineal múltiple, que incorpore variables como el tamaño de la casa, el vecindario y el número de dormitorios, probablemente proporcionará un modelo de predicción más preciso.
Regresión lineal versus regresión logística
La regresión lineal a menudo se confunde con la regresión logística. Mientras que la regresión lineal predice resultados en variablescontinuas, la regresión logística se utiliza cuando la variable dependiente escategórica, a menudo binaria (sí o no). Las variables categóricas definen grupos no numéricos con un número finito de categorías, como grupo de edad o método de pago. Las variables continuas, por otro lado, pueden tomar cualquier valor numérico y son mensurables. Ejemplos de variables continuas incluyen peso, precio y temperatura diaria.
A diferencia de la función lineal utilizada en la regresión lineal, la regresión logística modela la probabilidad de un resultado categórico utilizando una curva en forma de S llamada función logística. En el ejemplo de clasificación binaria, los puntos de datos que pertenecen a la categoría "sí" se encuentran en un lado de la forma de S, mientras que los puntos de datos de la categoría "no" se encuentran en el otro lado. En la práctica, la regresión logística se puede utilizar para clasificar si un correo electrónico es spam o no, o predecir si un cliente comprará un producto o no. Básicamente, la regresión lineal se utiliza para predecir valores cuantitativos, mientras que la regresión logística se utiliza para tareas de clasificación.
¿Cómo funciona la regresión lineal?
La regresión lineal funciona encontrando la línea que mejor se ajusta a través de un conjunto de puntos de datos. Este proceso implica:
1 Selección del modelo:En el primer paso, se selecciona la ecuación lineal adecuada para describir la relación entre las variables dependientes e independientes.
2 Ajuste del modelo:A continuación, se utiliza una técnica llamada Mínimos Cuadrados Ordinarios (OLS) para minimizar la suma de las diferencias al cuadrado entre los valores observados y los valores predichos por el modelo. Esto se hace ajustando la pendiente y la intersección de la línea para encontrar el mejor ajuste. El propósito de este método es minimizar el error o diferencia entre los valores previstos y reales. Este proceso de ajuste es una parte central del aprendizaje automático supervisado, en el que el modelo aprende de los datos de entrenamiento.

3 Evaluación del modelo:en el paso final, la calidad del ajuste se evalúa utilizando métricas como R-cuadrado, que mide la proporción de la varianza en la variable dependiente que es predecible a partir de las variables independientes. En otras palabras, R cuadrado mide qué tan bien se ajustan realmente los datos al modelo de regresión.
Este proceso genera un modelo de aprendizaje automático que luego se puede utilizar para hacer predicciones basadas en nuevos datos.
Aplicaciones de la regresión lineal en ML
En el aprendizaje automático, la regresión lineal es una herramienta comúnmente utilizada para predecir resultados y comprender las relaciones entre variables en varios campos. A continuación se muestran algunos ejemplos notables de sus aplicaciones:
Previsión del gasto del consumidor
Los niveles de ingresos se pueden utilizar en un modelo de regresión lineal para predecir el gasto de los consumidores. Específicamente, la regresión lineal múltiple podría incorporar factores como ingresos históricos, edad y situación laboral para proporcionar un análisis integral. Esto puede ayudar a los economistas a desarrollar políticas económicas basadas en datos y ayudar a las empresas a comprender mejor los patrones de comportamiento de los consumidores.
Analizar el impacto del marketing
Los especialistas en marketing pueden utilizar la regresión lineal para comprender cómo el gasto en publicidad afecta los ingresos por ventas. Al aplicar un modelo de regresión lineal a datos históricos, se pueden predecir los ingresos por ventas futuros, lo que permite a los especialistas en marketing optimizar sus presupuestos y estrategias publicitarias para lograr el máximo impacto.
Predecir los precios de las acciones
En el mundo de las finanzas, la regresión lineal es uno de los muchos métodos utilizados para predecir los precios de las acciones. Utilizando datos históricos de acciones y diversos indicadores económicos, los analistas e inversores pueden crear múltiples modelos de regresión lineal que les ayuden a tomar decisiones de inversión más inteligentes.
Previsión de las condiciones ambientales.
En ciencias ambientales, la regresión lineal se puede utilizar para pronosticar las condiciones ambientales. Por ejemplo, varios factores como el volumen de tráfico, las condiciones climáticas y la densidad de población pueden ayudar a predecir los niveles de contaminantes. Estos modelos de aprendizaje automático pueden ser utilizados por formuladores de políticas, científicos y otras partes interesadas para comprender y mitigar los impactos de diversas acciones en el medio ambiente.
Ventajas de la regresión lineal en ML
La regresión lineal ofrece varias ventajas que la convierten en una técnica clave en el aprendizaje automático.
Fácil de usar e implementar
En comparación con la mayoría de herramientas y modelos matemáticos, la regresión lineal es fácil de entender y aplicar. Es especialmente excelente como punto de partida para los nuevos profesionales del aprendizaje automático, ya que proporciona información y experiencia valiosas como base para algoritmos más avanzados.
Computacionalmente eficiente
Los modelos de aprendizaje automático pueden consumir muchos recursos. La regresión lineal requiere una potencia computacional relativamente baja en comparación con muchos algoritmos y aún puede proporcionar información predictiva significativa.
Resultados interpretables
Los modelos estadísticos avanzados, aunque potentes, suelen ser difíciles de interpretar. Con un modelo simple como la regresión lineal, la relación entre variables es fácil de entender y el impacto de cada variable está claramente indicado por su coeficiente.
Fundación para técnicas avanzadas.
Comprender e implementar la regresión lineal ofrece una base sólida para explorar métodos de aprendizaje automático más avanzados. Por ejemplo, la regresión polinómica se basa en la regresión lineal para describir relaciones no lineales más complejas entre variables.
Desventajas de la regresión lineal en ML
Si bien la regresión lineal es una herramienta valiosa en el aprendizaje automático, tiene varias limitaciones notables. Comprender estas desventajas es fundamental para seleccionar la herramienta de aprendizaje automático adecuada.
Suponiendo una relación lineal
El modelo de regresión lineal supone que la relación entre las variables dependientes e independientes es lineal. En escenarios complejos del mundo real, puede que este no sea siempre el caso. Por ejemplo, la altura de una persona a lo largo de su vida no es lineal: el rápido crecimiento que se produce durante la infancia se ralentiza y se detiene en la edad adulta. Por lo tanto, pronosticar la altura mediante regresión lineal podría generar predicciones inexactas.
Sensibilidad a los valores atípicos
Los valores atípicos son puntos de datos que se desvían significativamente de la mayoría de las observaciones en un conjunto de datos. Si no se manejan adecuadamente, estos puntos de valor extremo pueden sesgar los resultados y llevar a conclusiones inexactas. En el aprendizaje automático, esta sensibilidad significa que los valores atípicos pueden afectar de manera desproporcionada la precisión predictiva y la confiabilidad del modelo.
Multicolinealidad
En los modelos de regresión lineal múltiple, variables independientes altamente correlacionadas pueden distorsionar los resultados, fenómeno conocido comomulticolinealidad. Por ejemplo, el número de dormitorios de una casa y su tamaño pueden estar altamente correlacionados, ya que las casas más grandes tienden a tener más dormitorios. Esto puede dificultar la determinación del impacto individual de variables individuales en los precios de la vivienda, lo que lleva a resultados poco confiables.
Suponiendo una dispersión de error constante
La regresión lineal supone que las diferencias entre los valores observados y predichos (la dispersión del error) son las mismas para todas las variables independientes. Si esto no es cierto, las predicciones generadas por el modelo pueden no ser confiables. En el aprendizaje automático supervisado, no abordar la propagación del error puede hacer que el modelo genere estimaciones sesgadas e ineficientes, lo que reduce su eficacia general.
