Apa Regresi Linier dalam Pembelajaran Mesin?
Diterbitkan: 2024-09-06Regresi linier adalah teknik dasar dalam analisis data dan pembelajaran mesin (ML). Panduan ini akan membantu Anda memahami regresi linier, cara pembuatannya, serta jenis, penerapan, manfaat, dan kelemahannya.
Daftar isi
- Apa itu regresi linier?
- Jenis regresi linier
- Regresi linier vs. regresi logistik
- Bagaimana cara kerja regresi linier?
- Penerapan regresi linier
- Keuntungan regresi linier di ML
- Kekurangan regresi linier di ML
Apa itu regresi linier?
Regresi linier adalah metode statistik yang digunakan dalam pembelajaran mesin untuk memodelkan hubungan antara variabel terikat dan satu atau lebih variabel bebas. Ini memodelkan hubungan dengan menyesuaikan persamaan linier dengan data yang diamati, sering kali berfungsi sebagai titik awal untuk algoritma yang lebih kompleks dan banyak digunakan dalam analisis prediktif.
Pada dasarnya, regresi linier memodelkan hubungan antara variabel terikat (hasil yang ingin Anda prediksi) dan satu atau lebih variabel bebas (fitur masukan yang Anda gunakan untuk prediksi) dengan mencari garis lurus yang paling sesuai melalui sekumpulan titik data. Garis ini, yang disebutgaris regresi, mewakili hubungan antara variabel terikat (hasil yang ingin kita prediksi) dan variabel bebas (fitur masukan yang kita gunakan untuk prediksi). Persamaan garis regresi linier sederhana didefinisikan sebagai:
kamu = mx + c
dimana y adalah variabel terikat, x adalah variabel bebas, m adalah kemiringan garis, dan c adalah titik potong y. Persamaan ini memberikan model matematis untuk memetakan masukan ke keluaran yang diprediksi, dengan tujuan meminimalkan perbedaan antara nilai prediksi dan nilai observasi, yang dikenal sebagai residu. Dengan meminimalkan residu tersebut, regresi linier menghasilkan model yang paling mewakili data.
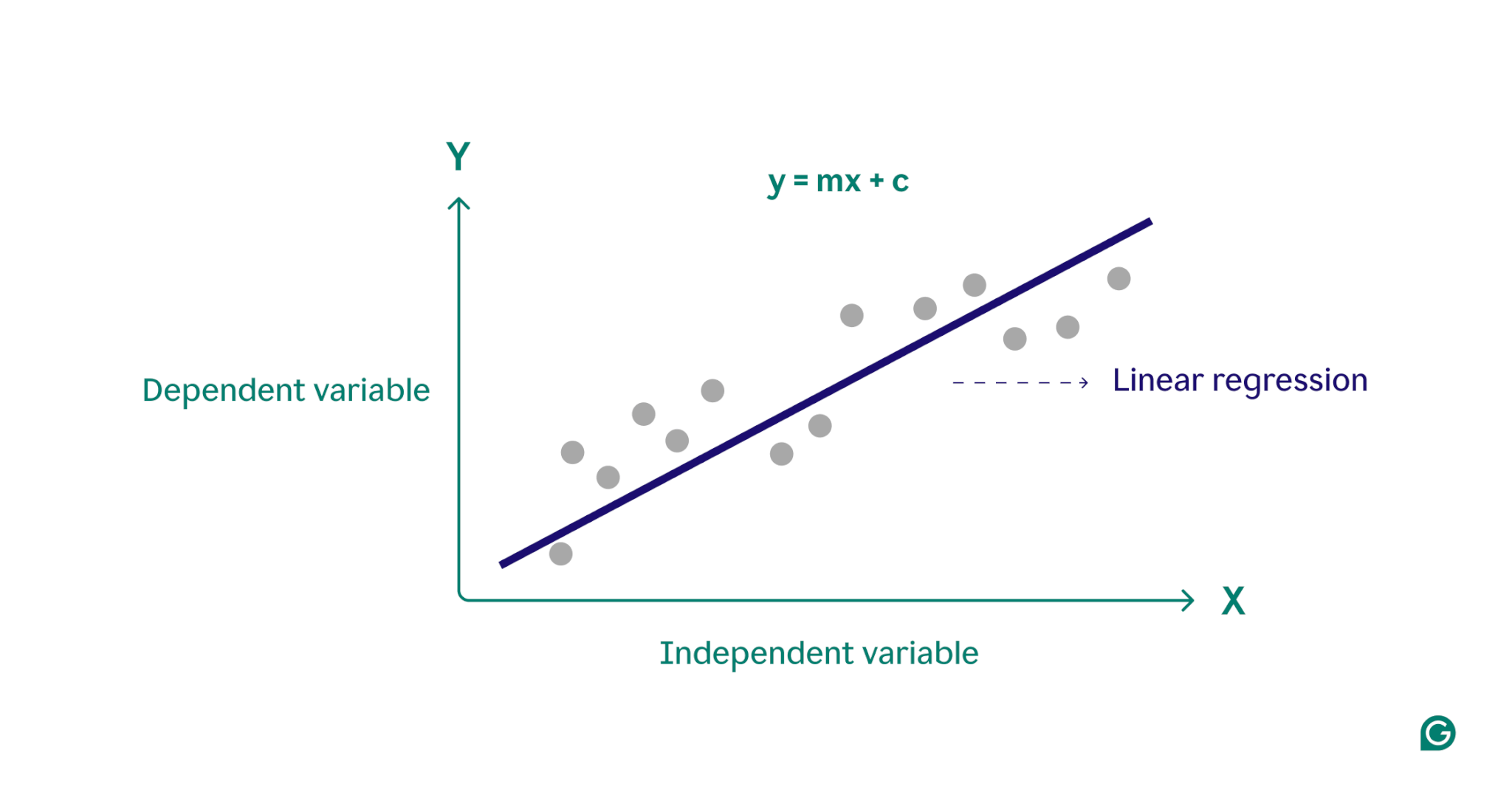
Secara konseptual, regresi linier dapat divisualisasikan sebagai menggambar garis lurus melalui titik-titik pada grafik untuk menentukan apakah terdapat hubungan antara titik-titik data tersebut. Model regresi linier yang ideal untuk sekumpulan titik data adalah garis yang paling mendekati nilai setiap titik dalam kumpulan data.
Jenis regresi linier
Ada dua jenis utama regresi linier:regresi linier sederhanadanregresi linier berganda.
Regresi linier sederhana
Regresi linier sederhana memodelkan hubungan antara satu variabel independen dengan variabel dependen dengan menggunakan garis lurus. Persamaan regresi linier sederhana adalah:
kamu = mx + c
dimana y adalah variabel terikat, x adalah variabel bebas, m adalah kemiringan garis, dan c adalah titik potong y.
Metode ini adalah cara mudah untuk mendapatkan wawasan yang jelas ketika berhadapan dengan skenario variabel tunggal. Pertimbangkan seorang dokter yang mencoba memahami bagaimana tinggi badan pasien mempengaruhi berat badan. Dengan memplot setiap variabel pada grafik dan menemukan garis yang paling sesuai menggunakan regresi linier sederhana, dokter dapat memprediksi berat badan pasien berdasarkan tinggi badannya saja.
Regresi linier berganda
Regresi linier berganda memperluas konsep regresi linier sederhana untuk mengakomodasi lebih dari satu variabel, sehingga memungkinkan dilakukannya analisis tentang bagaimana berbagai faktor mempengaruhi variabel terikat. Persamaan regresi linier berganda adalah:
y = b 0 + b 1 x 1 + b 2 x 2 + … + b n x n
dimana y adalah variabel terikat, x 1 , x 2 , …, x n adalah variabel bebas, dan b 1 , b 2 , …, b n adalah koefisien-koefisien yang menggambarkan hubungan antara masing-masing variabel bebas dan variabel terikat.
Sebagai contoh, perhatikan seorang agen real estate yang ingin memperkirakan harga rumah. Agen dapat menggunakan regresi linier sederhana berdasarkan satu variabel, seperti ukuran rumah atau kode pos, namun model ini terlalu sederhana, karena harga rumah sering kali didorong oleh interaksi kompleks dari berbagai faktor. Regresi linier berganda, yang menggabungkan variabel seperti ukuran rumah, lingkungan sekitar, dan jumlah kamar tidur, kemungkinan akan memberikan model prediksi yang lebih akurat.
Regresi linier vs. regresi logistik
Regresi linier sering disalahartikan dengan regresi logistik. Meskipun regresi linier memprediksi hasil pada variabelkontinu, regresi logistik digunakan jika variabel terikat bersifatkategoris, sering kali biner (ya atau tidak). Variabel kategori menentukan kelompok non-numerik dengan jumlah kategori terbatas, seperti kelompok usia atau metode pembayaran. Sebaliknya, variabel kontinu dapat mengambil nilai numerik apa pun dan dapat diukur. Contoh variabel kontinu meliputi berat, harga, dan suhu harian.
Berbeda dengan fungsi linier yang digunakan dalam regresi linier, regresi logistik memodelkan probabilitas hasil kategorikal menggunakan kurva berbentuk S yang disebut fungsi logistik. Dalam contoh klasifikasi biner, titik data yang termasuk dalam kategori “ya” berada di satu sisi bentuk S, sedangkan titik data dalam kategori “tidak” berada di sisi lainnya. Secara praktis, regresi logistik dapat digunakan untuk mengklasifikasikan apakah suatu email termasuk spam atau bukan, atau memprediksi apakah pelanggan akan membeli suatu produk atau tidak. Pada dasarnya, regresi linier digunakan untuk memprediksi nilai kuantitatif, sedangkan regresi logistik digunakan untuk tugas klasifikasi.
Bagaimana cara kerja regresi linier?
Regresi linier bekerja dengan menemukan garis yang paling sesuai melalui sekumpulan titik data. Proses ini melibatkan:
1 Memilih model:Pada langkah pertama, persamaan linier yang sesuai untuk menggambarkan hubungan antara variabel terikat dan bebas dipilih.
2 Menyesuaikan model:Selanjutnya, teknik yang disebut Ordinary Least Squares (OLS) digunakan untuk meminimalkan jumlah selisih kuadrat antara nilai yang diamati dan nilai yang diprediksi oleh model. Hal ini dilakukan dengan mengatur kemiringan dan perpotongan garis untuk menemukan yang paling sesuai. Tujuan dari metode ini adalah untuk meminimalkan kesalahan, atau perbedaan, antara nilai prediksi dan nilai sebenarnya. Proses penyesuaian ini adalah bagian inti dari pembelajaran mesin yang diawasi, di mana model belajar dari data pelatihan.

3 Mengevaluasi model:Pada langkah terakhir, kualitas kecocokan dinilai menggunakan metrik seperti R-squared, yang mengukur proporsi varians dalam variabel dependen yang dapat diprediksi dari variabel independen. Dengan kata lain, R-squared mengukur seberapa cocok data tersebut dengan model regresi.
Proses ini menghasilkan model pembelajaran mesin yang kemudian dapat digunakan untuk membuat prediksi berdasarkan data baru.
Penerapan regresi linier di ML
Dalam pembelajaran mesin, regresi linier adalah alat yang umum digunakan untuk memprediksi hasil dan memahami hubungan antar variabel di berbagai bidang. Berikut adalah beberapa contoh penting penerapannya:
Perkiraan belanja konsumen
Tingkat pendapatan dapat digunakan dalam model regresi linier untuk memprediksi belanja konsumen. Secara khusus, regresi linier berganda dapat memasukkan faktor-faktor seperti riwayat pendapatan, usia, dan status pekerjaan untuk memberikan analisis yang komprehensif. Hal ini dapat membantu para ekonom dalam mengembangkan kebijakan ekonomi berbasis data dan membantu dunia usaha lebih memahami pola perilaku konsumen.
Menganalisis dampak pemasaran
Pemasar dapat menggunakan regresi linier untuk memahami bagaimana pembelanjaan iklan memengaruhi pendapatan penjualan. Dengan menerapkan model regresi linier pada data historis, pendapatan penjualan di masa depan dapat diprediksi, sehingga memungkinkan pemasar mengoptimalkan anggaran dan strategi periklanan mereka untuk mendapatkan dampak maksimal.
Memprediksi harga saham
Dalam dunia keuangan, regresi linier merupakan salah satu dari sekian banyak metode yang digunakan untuk memprediksi harga saham. Dengan menggunakan data historis saham dan berbagai indikator ekonomi, analis dan investor dapat membangun model regresi linier berganda yang membantu mereka membuat keputusan investasi yang lebih cerdas.
Peramalan kondisi lingkungan
Dalam ilmu lingkungan, regresi linier dapat digunakan untuk meramalkan kondisi lingkungan. Misalnya, berbagai faktor seperti volume lalu lintas, kondisi cuaca, dan kepadatan penduduk dapat membantu memperkirakan tingkat polutan. Model pembelajaran mesin ini kemudian dapat digunakan oleh pembuat kebijakan, ilmuwan, dan pemangku kepentingan lainnya untuk memahami dan memitigasi dampak berbagai tindakan terhadap lingkungan.
Keuntungan regresi linier di ML
Regresi linier menawarkan beberapa keuntungan yang menjadikannya teknik utama dalam pembelajaran mesin.
Mudah digunakan dan diimplementasikan
Dibandingkan dengan kebanyakan alat dan model matematika, regresi linier mudah dipahami dan diterapkan. Hal ini sangat bagus terutama sebagai titik awal bagi praktisi pembelajaran mesin baru, memberikan wawasan dan pengalaman berharga sebagai landasan untuk algoritme yang lebih canggih.
Efisien secara komputasi
Model pembelajaran mesin bisa memakan banyak sumber daya. Regresi linier memerlukan daya komputasi yang relatif rendah dibandingkan dengan banyak algoritme dan masih dapat memberikan wawasan prediktif yang berarti.
Hasil yang dapat diinterpretasikan
Model statistik tingkat lanjut, meskipun kuat, seringkali sulit untuk ditafsirkan. Dengan model sederhana seperti regresi linier, hubungan antar variabel mudah dipahami, dan pengaruh setiap variabel ditunjukkan dengan jelas melalui koefisiennya.
Landasan untuk teknik tingkat lanjut
Memahami dan menerapkan regresi linier menawarkan dasar yang kuat untuk mengeksplorasi metode pembelajaran mesin yang lebih canggih. Misalnya, regresi polinomial dibangun di atas regresi linier untuk menggambarkan hubungan non-linier antar variabel yang lebih kompleks.
Kekurangan regresi linier di ML
Meskipun regresi linier adalah alat yang berharga dalam pembelajaran mesin, ia memiliki beberapa keterbatasan penting. Memahami kelemahan ini sangat penting dalam memilih alat pembelajaran mesin yang sesuai.
Dengan asumsi hubungan linier
Model regresi linier mengasumsikan hubungan antara variabel terikat dan bebas adalah linier. Dalam skenario dunia nyata yang kompleks, hal ini mungkin tidak selalu terjadi. Misalnya saja, tinggi badan seseorang sepanjang hidupnya bersifat nonlinier, dengan pertumbuhan cepat yang terjadi pada masa kanak-kanak melambat dan berhenti pada masa dewasa. Jadi, peramalan ketinggian menggunakan regresi linier dapat menyebabkan prediksi yang tidak akurat.
Sensitivitas terhadap outlier
Pencilan adalah titik data yang menyimpang secara signifikan dari sebagian besar observasi dalam kumpulan data. Jika tidak ditangani dengan benar, poin nilai ekstrem ini dapat mengubah hasil sehingga menghasilkan kesimpulan yang tidak akurat. Dalam pembelajaran mesin, sensitivitas ini berarti bahwa outlier dapat memengaruhi akurasi prediksi dan keandalan model secara tidak proporsional.
Multikolinearitas
Dalam model regresi linier berganda, variabel independen yang berkorelasi tinggi dapat mendistorsi hasil, sebuah fenomena yang dikenal sebagaimultikolinearitas. Misalnya, jumlah kamar tidur dalam sebuah rumah dan ukurannya mungkin sangat berkorelasi karena rumah yang lebih besar cenderung memiliki lebih banyak kamar tidur. Hal ini dapat mempersulit penentuan dampak masing-masing variabel terhadap harga perumahan, sehingga menghasilkan hasil yang tidak dapat diandalkan.
Dengan asumsi kesalahan menyebar secara konstan
Regresi linier mengasumsikan bahwa perbedaan antara nilai observasi dan prediksi (penyebaran kesalahan) adalah sama untuk semua variabel independen. Jika hal ini tidak benar, prediksi yang dihasilkan oleh model mungkin tidak dapat diandalkan. Dalam pembelajaran mesin yang diawasi, kegagalan mengatasi penyebaran kesalahan dapat menyebabkan model menghasilkan perkiraan yang bias dan tidak efisien, sehingga mengurangi efektivitasnya secara keseluruhan.
