Che cos'è la regressione lineare nell'apprendimento automatico?

La regressione lineare è una tecnica fondamentale nell'analisi dei dati e nell'apprendimento automatico (ML). Questa guida ti aiuterà a comprendere la regressione lineare, come è costruita e i suoi tipi, applicazioni, vantaggi e svantaggi.

Sommario

• Cos'è la regressione lineare?
• Tipi di regressione lineare
• Regressione lineare e regressione logistica
• Come funziona la regressione lineare?
• Applicazioni della regressione lineare
• Vantaggi della regressione lineare in ML
• Svantaggi della regressione lineare in ML

Cos'è la regressione lineare?

La regressione lineare è un metodo statistico utilizzato nell'apprendimento automatico per modellare la relazione tra una variabile dipendente e una o più variabili indipendenti. Modella le relazioni adattando un'equazione lineare ai dati osservati, spesso serve come punto di partenza per algoritmi più complessi ed è ampiamente utilizzato nell'analisi predittiva.

In sostanza, la regressione lineare modella la relazione tra una variabile dipendente (il risultato che si desidera prevedere) e una o più variabili indipendenti (le funzionalità di input utilizzate per la previsione) trovando la linea retta più adatta attraverso un insieme di punti dati. Questa linea, chiamatalinea di regressione, rappresenta la relazione tra la variabile dipendente (il risultato che vogliamo prevedere) e le variabili indipendenti (le caratteristiche di input che utilizziamo per la previsione). L'equazione per una retta di regressione lineare semplice è definita come:

y = mx + c

dove y è la variabile dipendente, x è la variabile indipendente, m è la pendenza della retta e c è l'intercetta y. Questa equazione fornisce un modello matematico per mappare gli input sugli output previsti, con l'obiettivo di ridurre al minimo le differenze tra i valori previsti e quelli osservati, noti come residui. Riducendo al minimo questi residui, la regressione lineare produce un modello che rappresenta al meglio i dati.

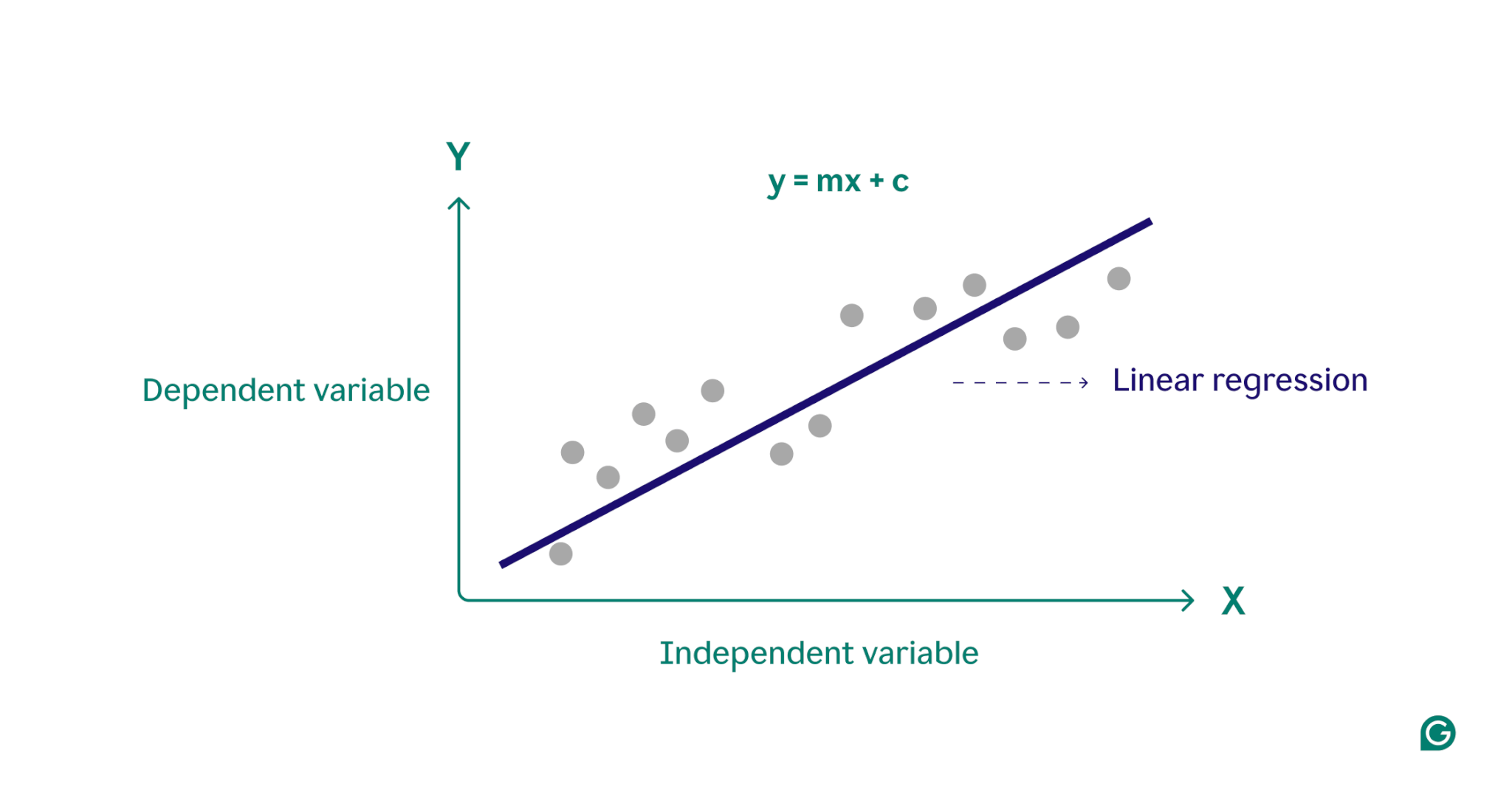
Concettualmente, la regressione lineare può essere visualizzata come il tracciamento di una linea retta che passa attraverso i punti su un grafico per determinare se esiste una relazione tra tali punti dati. Il modello di regressione lineare ideale per un insieme di punti dati è la linea che meglio approssima i valori di ogni punto nell'insieme di dati.

Tipi di regressione lineare

Esistono due tipi principali di regressione lineare:regressione lineare sempliceeregressione lineare multipla.

Regressione lineare semplice

La regressione lineare semplice modella la relazione tra una singola variabile indipendente e una variabile dipendente utilizzando una linea retta. L'equazione per la regressione lineare semplice è:

y = mx + c

dove y è la variabile dipendente, x è la variabile indipendente, m è la pendenza della retta e c è l'intercetta y.

Questo metodo è un modo semplice per ottenere informazioni chiare quando si affrontano scenari a variabile singola. Consideriamo un medico che cerca di capire in che modo l'altezza del paziente influisce sul peso. Tracciando ciascuna variabile su un grafico e trovando la linea più adatta utilizzando una semplice regressione lineare, il medico potrebbe prevedere il peso di un paziente basandosi solo sulla sua altezza.

Regressione lineare multipla

La regressione lineare multipla estende il concetto di regressione lineare semplice per includere più di una variabile, consentendo l'analisi di come più fattori influiscono sulla variabile dipendente. L'equazione per la regressione lineare multipla è:

y = b ₀ + b ₁ x ₁ + b ₂ x ₂ + … + b _n x _n

dove y è la variabile dipendente, x ₁ , x ₂ , …, x _n sono le variabili indipendenti e b ₁ , b ₂ , …, b _n sono i coefficienti che descrivono la relazione tra ciascuna variabile indipendente e la variabile dipendente.

Ad esempio, consideriamo un agente immobiliare che desidera stimare i prezzi delle case. L’agente potrebbe utilizzare una semplice regressione lineare basata su una singola variabile, come la dimensione della casa o il codice postale, ma questo modello sarebbe troppo semplicistico, poiché i prezzi delle case sono spesso guidati da una complessa interazione di molteplici fattori. Una regressione lineare multipla, che incorpori variabili come la dimensione della casa, il quartiere e il numero di camere da letto, fornirà probabilmente un modello di previsione più accurato.

Regressione lineare e regressione logistica

La regressione lineare viene spesso confusa con la regressione logistica. Mentre la regressione lineare prevede risultati su variabilicontinue, la regressione logistica viene utilizzata quando la variabile dipendente ècategoriale, spesso binaria (sì o no). Le variabili categoriali definiscono gruppi non numerici con un numero finito di categorie, come fascia di età o metodo di pagamento. Le variabili continue, invece, possono assumere qualsiasi valore numerico e sono misurabili. Esempi di variabili continue includono peso, prezzo e temperatura giornaliera.

A differenza della funzione lineare utilizzata nella regressione lineare, la regressione logistica modella la probabilità di un risultato categoriale utilizzando una curva a forma di S chiamata funzione logistica. Nell'esempio della classificazione binaria, i punti dati che appartengono alla categoria "sì" cadono su un lato della forma a S, mentre i punti dati nella categoria "no" cadono sull'altro lato. In pratica, la regressione logistica può essere utilizzata per classificare se un'e-mail è spam o meno o prevedere se un cliente acquisterà o meno un prodotto. Essenzialmente, la regressione lineare viene utilizzata per prevedere valori quantitativi, mentre la regressione logistica viene utilizzata per attività di classificazione.

Come funziona la regressione lineare?

La regressione lineare funziona trovando la linea più adatta attraverso una serie di punti dati. Questo processo comporta:

1 Selezione del modello:nella prima fase viene selezionata l'equazione lineare appropriata per descrivere la relazione tra le variabili dipendenti e indipendenti.

2 Adattamento del modello:Successivamente, viene utilizzata una tecnica chiamata Ordinary Least Squares (OLS) per ridurre al minimo la somma delle differenze al quadrato tra i valori osservati e i valori previsti dal modello. Questo viene fatto regolando la pendenza e l'intercettazione della linea per trovare la soluzione migliore. Lo scopo di questo metodo è ridurre al minimo l'errore, o la differenza, tra i valori previsti e quelli effettivi. Questo processo di adattamento è una parte fondamentale dell'apprendimento automatico supervisionato, in cui il modello apprende dai dati di addestramento.

3 Valutazione del modello:nella fase finale, la qualità dell'adattamento viene valutata utilizzando parametri come R-quadrato, che misura la proporzione della varianza nella variabile dipendente che è prevedibile dalle variabili indipendenti. In altre parole, l’R quadrato misura quanto bene i dati si adattano effettivamente al modello di regressione.

Questo processo genera un modello di apprendimento automatico che può quindi essere utilizzato per fare previsioni basate su nuovi dati.

Applicazioni della regressione lineare in ML

Nell'apprendimento automatico, la regressione lineare è uno strumento comunemente utilizzato per prevedere i risultati e comprendere le relazioni tra variabili in vari campi. Ecco alcuni esempi notevoli delle sue applicazioni:

Previsione della spesa dei consumatori

I livelli di reddito possono essere utilizzati in un modello di regressione lineare per prevedere la spesa dei consumatori. Nello specifico, la regressione lineare multipla potrebbe incorporare fattori quali reddito storico, età e condizione occupazionale per fornire un’analisi completa. Ciò può aiutare gli economisti a sviluppare politiche economiche basate sui dati e aiutare le aziende a comprendere meglio i modelli comportamentali dei consumatori.

Analisi dell'impatto del marketing

Gli esperti di marketing possono utilizzare la regressione lineare per comprendere in che modo la spesa pubblicitaria influisce sui ricavi delle vendite. Applicando un modello di regressione lineare ai dati storici, è possibile prevedere i futuri ricavi delle vendite, consentendo agli esperti di marketing di ottimizzare i propri budget e le strategie pubblicitarie per ottenere il massimo impatto.

Prevedere i prezzi delle azioni

Nel mondo finanziario, la regressione lineare è uno dei tanti metodi utilizzati per prevedere i prezzi delle azioni. Utilizzando dati azionari storici e vari indicatori economici, analisti e investitori possono costruire più modelli di regressione lineare che li aiutano a prendere decisioni di investimento più intelligenti.

Previsione delle condizioni ambientali

Nelle scienze ambientali, la regressione lineare può essere utilizzata per prevedere le condizioni ambientali. Ad esempio, vari fattori come il volume del traffico, le condizioni meteorologiche e la densità della popolazione possono aiutare a prevedere i livelli di inquinamento. Questi modelli di apprendimento automatico possono quindi essere utilizzati da politici, scienziati e altre parti interessate per comprendere e mitigare gli impatti di varie azioni sull’ambiente.

Vantaggi della regressione lineare in ML

La regressione lineare offre numerosi vantaggi che la rendono una tecnica chiave nell'apprendimento automatico.

Semplice da usare e implementare

Rispetto alla maggior parte degli strumenti e modelli matematici, la regressione lineare è facile da comprendere e applicare. È particolarmente utile come punto di partenza per i nuovi professionisti del machine learning, poiché fornisce preziose informazioni ed esperienza come base per algoritmi più avanzati.

Computazionalmente efficiente

I modelli di machine learning possono richiedere un utilizzo intensivo delle risorse. La regressione lineare richiede una potenza di calcolo relativamente bassa rispetto a molti algoritmi e può comunque fornire informazioni predittive significative.

Risultati interpretabili

I modelli statistici avanzati, sebbene potenti, sono spesso difficili da interpretare. Con un modello semplice come la regressione lineare, la relazione tra le variabili è facile da comprendere e l’impatto di ciascuna variabile è chiaramente indicato dal suo coefficiente.

Fondazione per tecniche avanzate

Comprendere e implementare la regressione lineare offre una solida base per esplorare metodi di machine learning più avanzati. Ad esempio, la regressione polinomiale si basa sulla regressione lineare per descrivere relazioni più complesse e non lineari tra le variabili.

Svantaggi della regressione lineare in ML

Sebbene la regressione lineare sia uno strumento prezioso nell'apprendimento automatico, presenta diverse limitazioni notevoli. Comprendere questi svantaggi è fondamentale per selezionare lo strumento di machine learning appropriato.

Supponendo una relazione lineare

Il modello di regressione lineare presuppone che la relazione tra variabili dipendenti e indipendenti sia lineare. In scenari reali complessi, questo potrebbe non essere sempre il caso. Ad esempio, l'altezza di una persona nel corso della sua vita non è lineare, con la rapida crescita che si verifica durante l'infanzia che rallenta e si ferma nell'età adulta. Pertanto, prevedere l'altezza utilizzando la regressione lineare potrebbe portare a previsioni imprecise.

Sensibilità ai valori anomali

I valori anomali sono punti dati che si discostano in modo significativo dalla maggior parte delle osservazioni in un set di dati. Se non gestiti correttamente, questi valori estremi possono distorcere i risultati, portando a conclusioni imprecise. Nell'apprendimento automatico, questa sensibilità significa che i valori anomali possono influenzare in modo sproporzionato l'accuratezza predittiva e l'affidabilità del modello.

Multicollinearità

Nei modelli di regressione lineare multipla, variabili indipendenti altamente correlate possono distorcere i risultati, un fenomeno noto comemulticollinearità. Ad esempio, il numero di camere da letto in una casa e le sue dimensioni potrebbero essere altamente correlati poiché le case più grandi tendono ad avere più camere da letto. Ciò può rendere difficile determinare l’impatto individuale delle singole variabili sui prezzi delle case, portando a risultati inaffidabili.

Supponendo una diffusione dell'errore costante

La regressione lineare presuppone che le differenze tra i valori osservati e quelli previsti (lo spread di errore) siano le stesse per tutte le variabili indipendenti. Se ciò non è vero, le previsioni generate dal modello potrebbero essere inaffidabili. Nell’apprendimento automatico supervisionato, la mancata gestione della diffusione degli errori può far sì che il modello generi stime distorte e inefficienti, riducendone l’efficacia complessiva.