機械学習における線形回帰とは何ですか?
公開: 2024-09-06線形回帰は、データ分析と機械学習 (ML) の基本的な手法です。このガイドは、線形回帰、その構築方法、その種類、用途、利点、欠点を理解するのに役立ちます。
目次
- 線形回帰とは何ですか?
- 線形回帰の種類
- 線形回帰とロジスティック回帰
- 線形回帰はどのように機能するのでしょうか?
- 線形回帰の応用
- ML における線形回帰の利点
- ML における線形回帰の欠点
線形回帰とは何ですか?
線形回帰は、従属変数と 1 つ以上の独立変数の間の関係をモデル化するために機械学習で使用される統計手法です。観測データに線形方程式を当てはめることによって関係をモデル化します。多くの場合、より複雑なアルゴリズムの開始点として機能し、予測分析で広く使用されます。
基本的に、線形回帰は、データ ポイントのセットを通じて最適な直線を見つけることによって、従属変数 (予測する結果) と 1 つ以上の独立変数 (予測に使用する入力特徴) の間の関係をモデル化します。この線は回帰直線と呼ばれ、従属変数 (予測したい結果) と独立変数 (予測に使用する入力特徴) の間の関係を表します。単純な線形回帰直線の方程式は次のように定義されます。
y = mx + c
ここで、 yは従属変数、 xは独立変数、m は直線の傾き、 c はy 切片です。この方程式は、残差として知られる予測値と観測値の差を最小限に抑えることを目的として、入力を予測出力にマッピングするための数学的モデルを提供します。これらの残差を最小限に抑えることで、線形回帰はデータを最もよく表すモデルを生成します。
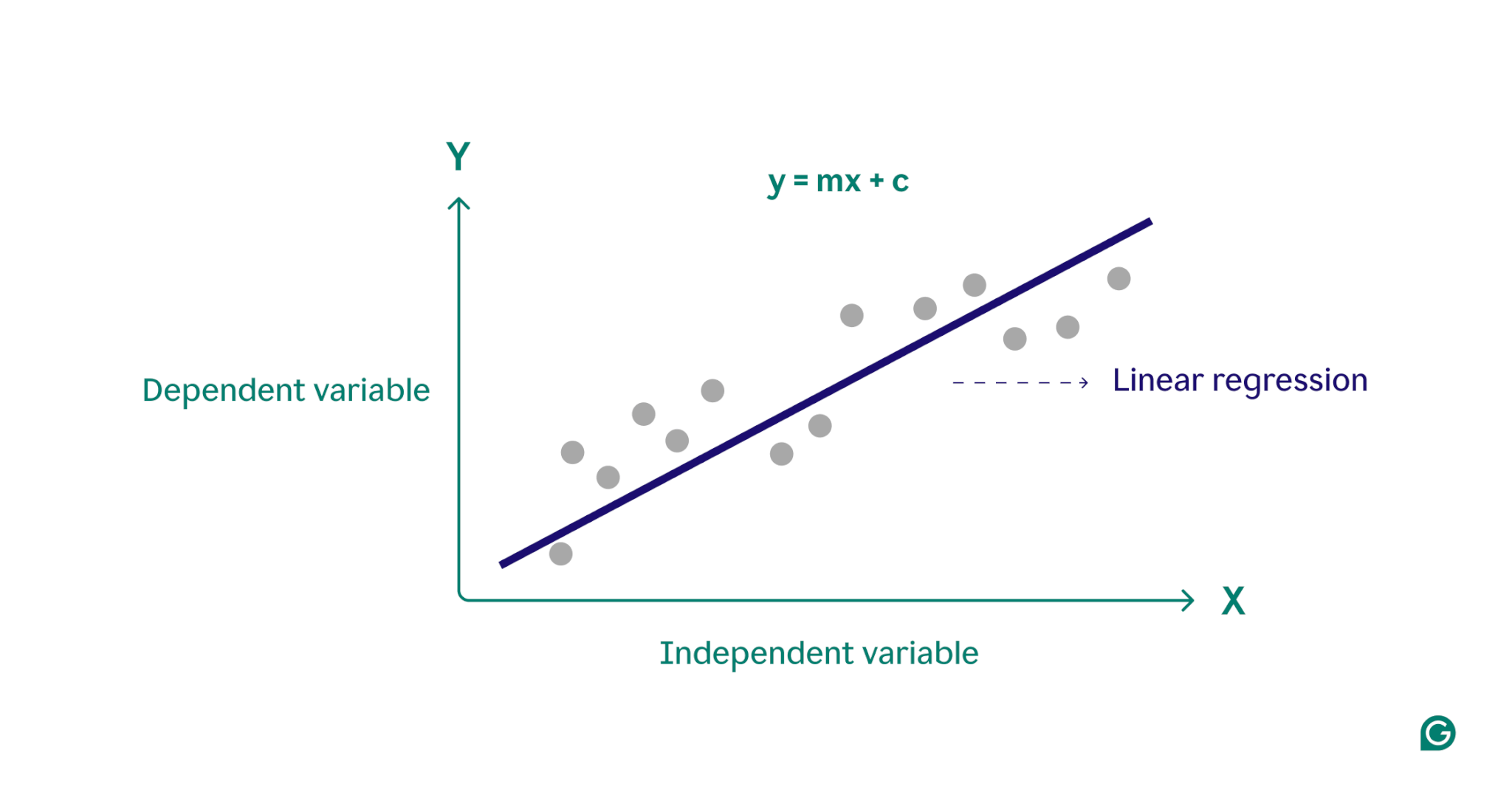
概念的には、線形回帰は、グラフ上の点を通る直線を引いて、それらのデータ点間に関係があるかどうかを判断するものとして視覚化できます。データ ポイントのセットに対する理想的な線形回帰モデルは、データ セット内のすべてのポイントの値を最もよく近似する直線です。
線形回帰の種類
線形回帰には、単純線形回帰と多重線形回帰の 2 つの主なタイプがあります。
単純な線形回帰
単純な線形回帰は、単一の独立変数と従属変数の間の関係を直線を使用してモデル化します。単純な線形回帰の方程式は次のとおりです。
y = mx + c
ここで、 yは従属変数、 xは独立変数、 mは直線の傾き、 c はy 切片です。
この方法は、単一変数のシナリオを扱う場合に明確な洞察を得る簡単な方法です。患者の身長が体重にどのような影響を与えるかを理解しようとしている医師のことを考えてみましょう。各変数をグラフ上にプロットし、単純な線形回帰を使用して最適な直線を見つけることにより、医師は患者の身長のみに基づいて患者の体重を予測できます。
多重線形回帰
多重線形回帰は、単純な線形回帰の概念を複数の変数に対応できるように拡張し、複数の要因が従属変数にどのような影響を与えるかを分析できるようにします。重線形回帰の方程式は次のとおりです。
y = b 0 + b 1 x 1 + b 2 x 2 + … + b n x n
ここで、 yは従属変数、 x 1 、x 2 、…、 x nは独立変数、 b 1 、b 2 、…、 b n は各独立変数と従属変数の間の関係を記述する係数です。
例として、住宅価格を見積もりたい不動産業者について考えてみましょう。エージェントは、家の大きさや郵便番号などの単一変数に基づく単純な線形回帰を使用できますが、住宅価格は複数の要因の複雑な相互作用によって左右されることが多いため、このモデルは単純すぎます。家の大きさ、近所、寝室の数などの変数を組み込んだ重線形回帰は、より正確な予測モデルを提供する可能性があります。
線形回帰とロジスティック回帰
線形回帰は、ロジスティック回帰と混同されることがよくあります。線形回帰は連続変数の結果を予測しますが、ロジスティック回帰は、従属変数がカテゴリカル(多くの場合 2 値 (はいまたはいいえ)) の場合に使用されます。カテゴリ変数は、年齢グループや支払い方法など、有限数のカテゴリを持つ非数値グループを定義します。一方、連続変数は任意の数値を取ることができ、測定可能です。連続変数の例には、重量、価格、毎日の気温などがあります。
線形回帰で使用される線形関数とは異なり、ロジスティック回帰では、ロジスティック関数と呼ばれる S 字曲線を使用してカテゴリカルな結果の確率をモデル化します。バイナリ分類の例では、「はい」カテゴリに属するデータ ポイントは S 字型の一方の側にあり、「いいえ」カテゴリのデータ ポイントは反対側にあります。実際には、ロジスティック回帰を使用して、電子メールがスパムであるかどうかを分類したり、顧客が製品を購入するかどうかを予測したりできます。基本的に、線形回帰は定量値の予測に使用され、ロジスティック回帰は分類タスクに使用されます。

線形回帰はどのように機能するのでしょうか?
線形回帰は、一連のデータ ポイントを通じて最適な直線を見つけることによって機能します。このプロセスには以下が含まれます。
1モデルの選択:最初のステップでは、従属変数と独立変数の間の関係を記述する適切な線形方程式が選択されます。
2モデルのフィッティング:次に、通常最小二乗法 (OLS) と呼ばれる手法を使用して、観測値とモデルによって予測された値の差の二乗の合計を最小化します。これは、線の傾きと切片を調整して最適なフィットを見つけることによって行われます。この方法の目的は、予測値と実際の値の間の誤差または差異を最小限に抑えることです。このフィッティング プロセスは教師あり機械学習の中核部分であり、モデルはトレーニング データから学習します。
3モデルの評価:最終ステップでは、独立変数から予測可能な従属変数の分散の割合を測定する R 二乗などの指標を使用して適合の質が評価されます。言い換えれば、R 二乗は、データが実際に回帰モデルにどの程度適合しているかを測定します。
このプロセスにより、新しいデータに基づいた予測を行うために使用できる機械学習モデルが生成されます。
ML における線形回帰の応用
機械学習では、線形回帰は、結果を予測し、さまざまな分野にわたる変数間の関係を理解するために一般的に使用されるツールです。以下に、その応用例のいくつかの注目すべき例を示します。
消費者支出の予測
所得レベルを線形回帰モデルで使用して、消費者支出を予測できます。具体的には、多重線形回帰では、過去の収入、年齢、雇用状況などの要素を組み込んで、包括的な分析を行うことができます。これは、経済学者がデータ主導の経済政策を開発するのに役立ち、企業が消費者の行動パターンをより深く理解するのに役立ちます。
マーケティングへの影響を分析する
マーケティング担当者は線形回帰を使用して、広告支出が売上収益にどのような影響を与えるかを理解できます。線形回帰モデルを履歴データに適用することで、将来の売上収益を予測できるため、マーケティング担当者は予算と広告戦略を最適化して最大限の効果を得ることができます。
株価の予測
金融の世界では、線形回帰は株価を予測するために使用される多くの方法の 1 つです。過去の株価データやさまざまな経済指標を使用して、アナリストや投資家は、より賢明な投資決定を下すのに役立つ複数の線形回帰モデルを構築できます。
環境条件の予測
環境科学では、線形回帰を使用して環境条件を予測できます。たとえば、交通量、気象条件、人口密度などのさまざまな要因は、汚染物質レベルの予測に役立ちます。これらの機械学習モデルは、政策立案者、科学者、その他の関係者が環境に対するさまざまな行動の影響を理解し、軽減するために使用できます。
ML における線形回帰の利点
線形回帰にはいくつかの利点があり、機械学習における重要な手法となっています。
使い方も実装も簡単
ほとんどの数学ツールやモデルと比較して、線形回帰は理解しやすく、適用しやすいです。これは、新しい機械学習の実践者にとっての出発点として特に優れており、より高度なアルゴリズムの基盤として貴重な洞察と経験を提供します。
計算効率が高い
機械学習モデルはリソースを大量に消費する可能性があります。線形回帰は、多くのアルゴリズムと比較して比較的低い計算能力を必要とし、それでも有意義な予測洞察を提供できます。
解釈可能な結果
高度な統計モデルは強力ですが、多くの場合解釈が困難です。線形回帰のような単純なモデルでは、変数間の関係が理解しやすく、各変数の影響がその係数によって明確に示されます。
高度な技術の基礎
線形回帰を理解して実装すると、より高度な機械学習手法を探求するための強固な基盤が得られます。たとえば、多項式回帰は線形回帰に基づいて、変数間のより複雑な非線形関係を記述します。
ML における線形回帰の欠点
線形回帰は機械学習における貴重なツールですが、いくつかの注目すべき制限があります。適切な機械学習ツールを選択するには、これらの欠点を理解することが重要です。
線形関係を仮定すると
線形回帰モデルは、従属変数と独立変数の間の関係が線形であることを前提としています。現実の複雑なシナリオでは、これが常に当てはまるとは限りません。たとえば、人の身長は生涯を通じて非線形であり、小児期に急速に成長した成長は成人期に減速して停止します。したがって、線形回帰を使用して高さを予測すると、不正確な予測につながる可能性があります。
外れ値に対する感度
外れ値は、データセット内の観測値の大部分から大きく逸脱したデータ ポイントです。適切に処理しないと、これらの極端な値のポイントによって結果が歪められ、不正確な結論が得られる可能性があります。機械学習では、この感度は、外れ値がモデルの予測精度と信頼性に不釣り合いな影響を与える可能性があることを意味します。
多重共線性
多重線形回帰モデルでは、相関性の高い独立変数によって結果が歪む可能性があり、これは多重共線性として知られる現象です。たとえば、大きな家には寝室の数が多くなる傾向があるため、家の寝室の数とその広さには高度な相関関係がある可能性があります。このため、住宅価格に対する個々の変数の個別の影響を判断することが困難になり、信頼性の低い結果につながる可能性があります。
誤差の広がりが一定であると仮定すると
線形回帰では、観測値と予測値の差 (誤差の広がり) がすべての独立変数で同じであると仮定します。これが当てはまらない場合、モデルによって生成された予測は信頼できない可能性があります。教師あり機械学習では、誤差の広がりに対処できないと、モデルが偏った非効率な推定値を生成し、全体的な有効性が低下する可能性があります。
