Co to jest regresja liniowa w uczeniu maszynowym?

Regresja liniowa to podstawowa technika analizy danych i uczenia maszynowego (ML). Ten przewodnik pomoże Ci zrozumieć regresję liniową, jej budowę, rodzaje, zastosowania, zalety i wady.

Spis treści

• Co to jest regresja liniowa?
• Rodzaje regresji liniowej
• Regresja liniowa a regresja logistyczna
• Jak działa regresja liniowa?
• Zastosowania regresji liniowej
• Zalety regresji liniowej w ML
• Wady regresji liniowej w ML

Co to jest regresja liniowa?

Regresja liniowa to metoda statystyczna stosowana w uczeniu maszynowym do modelowania relacji między zmienną zależną a jedną lub większą liczbą zmiennych niezależnych. Modeluje zależności, dopasowując równanie liniowe do obserwowanych danych, często służąc jako punkt wyjścia dla bardziej złożonych algorytmów i jest szeroko stosowany w analizie predykcyjnej.

Zasadniczo regresja liniowa modeluje relację między zmienną zależną (wynikiem, który chcesz przewidzieć) a jedną lub większą liczbą zmiennych niezależnych (cechami wejściowymi używanymi do prognozowania) poprzez znalezienie najlepiej dopasowanej linii prostej przechodzącej przez zestaw punktów danych. Linia ta, zwanalinią regresji, przedstawia relację pomiędzy zmienną zależną (wynikiem, który chcemy przewidzieć) a zmiennymi niezależnymi (cechami wejściowymi, których używamy do przewidywania). Równanie prostej linii regresji liniowej definiuje się jako:

y = mx + do

gdzie y jest zmienną zależną, x jest zmienną niezależną, m jest nachyleniem linii, a c jest punktem przecięcia z y. Równanie to zapewnia model matematyczny do mapowania danych wejściowych na przewidywane wyniki, którego celem jest minimalizowanie różnic między wartościami przewidywanymi i obserwowanymi, zwanych resztami. Minimalizując te reszty, regresja liniowa tworzy model, który najlepiej reprezentuje dane.

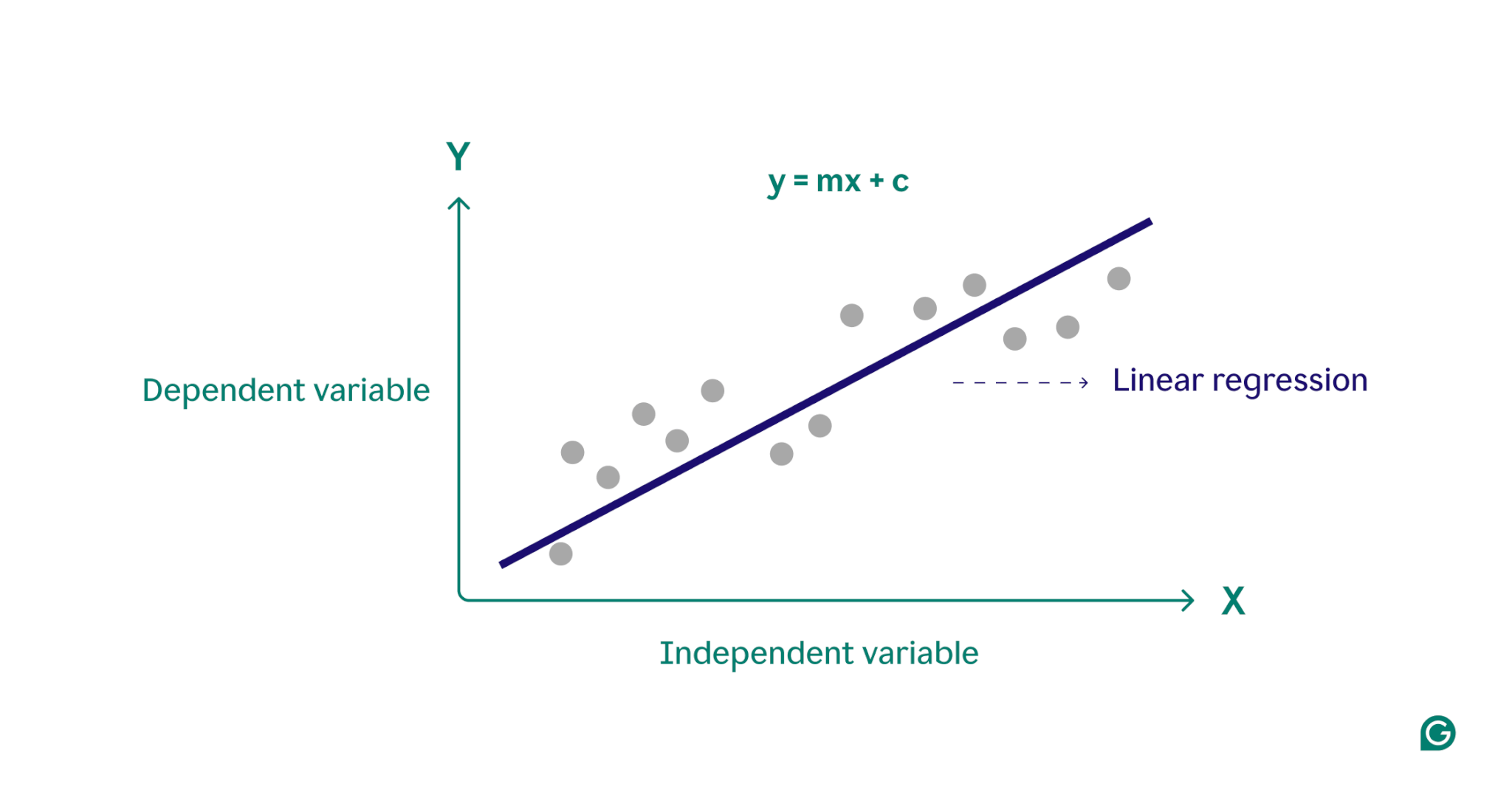
Koncepcyjnie regresję liniową można sobie wyobrazić jako rysowanie linii prostej przez punkty na wykresie w celu ustalenia, czy istnieje związek między tymi punktami danych. Idealny model regresji liniowej dla zbioru punktów danych to linia, która najlepiej przybliża wartości każdego punktu w zbiorze danych.

Rodzaje regresji liniowej

Istnieją dwa główne typy regresji liniowej:prosta regresja liniowaiwielokrotna regresja liniowa.

Prosta regresja liniowa

Prosta regresja liniowa modeluje relację pomiędzy pojedynczą zmienną niezależną a zmienną zależną za pomocą linii prostej. Równanie prostej regresji liniowej wygląda następująco:

y = mx + do

gdzie y jest zmienną zależną, x jest zmienną niezależną, m jest nachyleniem linii, a c jest punktem przecięcia z y.

Ta metoda to prosty sposób na uzyskanie jasnych wniosków w przypadku scenariuszy z jedną zmienną. Weźmy pod uwagę lekarza próbującego zrozumieć, jak wzrost pacjenta wpływa na wagę. Wykreślając każdą zmienną na wykresie i znajdując najlepiej dopasowaną linię za pomocą prostej regresji liniowej, lekarz mógł przewidzieć wagę pacjenta na podstawie samego jego wzrostu.

Wielokrotna regresja liniowa

Wielokrotna regresja liniowa rozszerza koncepcję prostej regresji liniowej, aby uwzględnić więcej niż jedną zmienną, umożliwiając analizę wpływu wielu czynników na zmienną zależną. Równanie wielokrotnej regresji liniowej wygląda następująco:

y = b ₀ + b ₁ x ₁ + b ₂ x ₂ + … + b _n x _n

gdzie y jest zmienną zależną, x ₁ , x ₂ , …, x _n to zmienne niezależne, a b ₁ , b ₂ , …, b _n to współczynniki opisujące związek pomiędzy każdą zmienną niezależną a zmienną zależną.

Jako przykład rozważmy agenta nieruchomości, który chce oszacować ceny domów. Agent mógłby zastosować prostą regresję liniową opartą na pojedynczej zmiennej, takiej jak wielkość domu lub kod pocztowy, ale ten model byłby zbyt uproszczony, ponieważ ceny mieszkań często zależą od złożonej interakcji wielu czynników. Wielokrotna regresja liniowa obejmująca zmienne takie jak wielkość domu, sąsiedztwo i liczba sypialni prawdopodobnie zapewni dokładniejszy model predykcyjny.

Regresja liniowa a regresja logistyczna

Regresja liniowa jest często mylona z regresją logistyczną. Podczas gdy regresja liniowa przewiduje wyniki dla zmiennychciągłych, regresję logistyczną stosuje się, gdy zmienna zależna jestkategoryczna, często binarna (tak lub nie). Zmienne kategoryczne definiują grupy nieliczbowe ze skończoną liczbą kategorii, takich jak grupa wiekowa lub metoda płatności. Natomiast zmienne ciągłe mogą przyjmować dowolną wartość liczbową i są mierzalne. Przykładami zmiennych ciągłych są waga, cena i dzienna temperatura.

W przeciwieństwie do funkcji liniowej stosowanej w regresji liniowej, regresja logistyczna modeluje prawdopodobieństwo wystąpienia kategorycznego wyniku za pomocą krzywej w kształcie litery S zwanej funkcją logistyczną. W przykładzie klasyfikacji binarnej punkty danych należące do kategorii „tak” znajdują się po jednej stronie kształtu S, podczas gdy punkty danych należące do kategorii „nie” znajdują się po drugiej stronie. W praktyce regresję logistyczną można zastosować do klasyfikacji, czy wiadomość e-mail jest spamem, czy nie, lub do przewidywania, czy klient kupi produkt, czy nie. Zasadniczo regresję liniową stosuje się do przewidywania wartości ilościowych, natomiast regresję logistyczną stosuje się do zadań klasyfikacyjnych.

Jak działa regresja liniowa?

Regresja liniowa polega na znalezieniu najlepiej dopasowanej linii przechodzącej przez zbiór punktów danych. Proces ten obejmuje:

1 Wybór modelu:W pierwszym kroku wybierane jest odpowiednie równanie liniowe opisujące zależność pomiędzy zmiennymi zależnymi i niezależnymi.

2 Dopasowanie modelu:Następnie stosuje się technikę zwaną zwykłymi najmniejszymi kwadratami (OLS), aby zminimalizować sumę kwadratów różnic pomiędzy wartościami obserwowanymi i wartościami przewidywanymi przez model. Odbywa się to poprzez dostosowanie nachylenia i punktu przecięcia linii w celu znalezienia najlepszego dopasowania. Celem tej metody jest zminimalizowanie błędu lub różnicy pomiędzy wartościami przewidywanymi i rzeczywistymi. Ten proces dopasowywania jest podstawową częścią nadzorowanego uczenia maszynowego, w którym model uczy się na podstawie danych szkoleniowych.

3 Ocena modelu:Na ostatnim etapie ocenia się jakość dopasowania przy użyciu takich metryk, jak R-kwadrat, który mierzy proporcję wariancji zmiennej zależnej przewidywalną na podstawie zmiennych niezależnych. Innymi słowy, R-kwadrat mierzy, jak dobrze dane faktycznie pasują do modelu regresji.

Ten proces generuje model uczenia maszynowego, który można następnie wykorzystać do przewidywania na podstawie nowych danych.

Zastosowania regresji liniowej w ML

W uczeniu maszynowym regresja liniowa jest powszechnie używanym narzędziem do przewidywania wyników i zrozumienia zależności między zmiennymi w różnych dziedzinach. Oto kilka godnych uwagi przykładów jego zastosowań:

Prognozowanie wydatków konsumenckich

Poziomy dochodów można wykorzystać w modelu regresji liniowej do przewidywania wydatków konsumenckich. W szczególności wielokrotna regresja liniowa może uwzględniać takie czynniki, jak dochód historyczny, wiek i status zatrudnienia, aby zapewnić wszechstronną analizę. Może to pomóc ekonomistom w opracowywaniu polityk gospodarczych opartych na danych i pomóc przedsiębiorstwom lepiej zrozumieć wzorce zachowań konsumentów.

Analiza wpływu marketingowego

Marketerzy mogą zastosować regresję liniową, aby zrozumieć, jak wydatki na reklamę wpływają na przychody ze sprzedaży. Stosując model regresji liniowej do danych historycznych, można przewidzieć przyszłe przychody ze sprzedaży, umożliwiając marketerom optymalizację budżetów i strategii reklamowych w celu uzyskania maksymalnego efektu.

Przewidywanie cen akcji

W świecie finansów regresja liniowa jest jedną z wielu metod stosowanych do przewidywania cen akcji. Korzystając z historycznych danych giełdowych i różnych wskaźników ekonomicznych, analitycy i inwestorzy mogą budować wiele modeli regresji liniowej, które pomagają im podejmować mądrzejsze decyzje inwestycyjne.

Prognozowanie warunków środowiskowych

W naukach o środowisku regresję liniową można zastosować do prognozowania warunków środowiskowych. Na przykład różne czynniki, takie jak natężenie ruchu, warunki pogodowe i gęstość zaludnienia, mogą pomóc w przewidywaniu poziomu substancji zanieczyszczających. Te modele uczenia maszynowego mogą następnie zostać wykorzystane przez decydentów, naukowców i inne zainteresowane strony do zrozumienia i łagodzenia wpływu różnych działań na środowisko.

Zalety regresji liniowej w ML

Regresja liniowa ma kilka zalet, które czynią ją kluczową techniką w uczeniu maszynowym.

Prosty w użyciu i wdrożeniu

W porównaniu z większością narzędzi i modeli matematycznych regresja liniowa jest łatwa do zrozumienia i zastosowania. Jest szczególnie świetny jako punkt wyjścia dla nowych praktyków uczenia maszynowego, zapewniając cenne spostrzeżenia i doświadczenie jako podstawę dla bardziej zaawansowanych algorytmów.

Wydajny obliczeniowo

Modele uczenia maszynowego mogą wymagać dużych zasobów. Regresja liniowa wymaga stosunkowo małej mocy obliczeniowej w porównaniu z wieloma algorytmami, a mimo to może zapewnić znaczące spostrzeżenia predykcyjne.

Interpretowalne wyniki

Zaawansowane modele statystyczne, choć potężne, często są trudne do interpretacji. Dzięki prostemu modelowi, takiemu jak regresja liniowa, związek między zmiennymi jest łatwy do zrozumienia, a wpływ każdej zmiennej jest wyraźnie wskazany przez jej współczynnik.

Podstawa zaawansowanych technik

Zrozumienie i wdrożenie regresji liniowej stanowi solidną podstawę do odkrywania bardziej zaawansowanych metod uczenia maszynowego. Na przykład regresja wielomianowa opiera się na regresji liniowej w celu opisania bardziej złożonych, nieliniowych relacji między zmiennymi.

Wady regresji liniowej w ML

Chociaż regresja liniowa jest cennym narzędziem w uczeniu maszynowym, ma kilka znaczących ograniczeń. Zrozumienie tych wad ma kluczowe znaczenie przy wyborze odpowiedniego narzędzia do uczenia maszynowego.

Zakładając zależność liniową

Model regresji liniowej zakłada, że ​​związek pomiędzy zmiennymi zależnymi i niezależnymi ma charakter liniowy. W złożonych scenariuszach rzeczywistych nie zawsze tak jest. Na przykład wzrost człowieka w ciągu jego życia jest nieliniowy, a szybki wzrost występujący w dzieciństwie zwalnia i zatrzymuje się w wieku dorosłym. Zatem prognozowanie wzrostu za pomocą regresji liniowej może prowadzić do niedokładnych przewidywań.

Wrażliwość na wartości odstające

Wartości odstające to punkty danych, które znacząco odbiegają od większości obserwacji w zbiorze danych. Jeśli nie zostaną właściwie potraktowane, te skrajne wartości mogą wypaczyć wyniki, prowadząc do niedokładnych wniosków. W uczeniu maszynowym ta czułość oznacza, że ​​wartości odstające mogą nieproporcjonalnie wpływać na dokładność predykcyjną i niezawodność modelu.

Wielowspółliniowość

W modelach wielokrotnej regresji liniowej silnie skorelowane zmienne niezależne mogą zniekształcać wyniki, co jest zjawiskiem znanym jakowielowspółliniowość. Na przykład liczba sypialni w domu i jego wielkość mogą być silnie powiązane, ponieważ większe domy mają zwykle więcej sypialni. Może to utrudniać określenie indywidualnego wpływu poszczególnych zmiennych na ceny mieszkań, prowadząc do niewiarygodnych wyników.

Zakładając stały rozkład błędów

Regresja liniowa zakłada, że ​​różnice pomiędzy wartościami obserwowanymi i przewidywanymi (rozrzut błędów) są takie same dla wszystkich zmiennych niezależnych. Jeżeli nie jest to prawdą, przewidywania generowane przez model mogą być niewiarygodne. W nadzorowanym uczeniu maszynowym brak rozwiązania problemu rozprzestrzeniania się błędów może spowodować, że model będzie generował stronnicze i nieefektywne szacunki, zmniejszając jego ogólną skuteczność.