Ce este regresia liniară în învățarea automată?

Regresia liniară este o tehnică de bază în analiza datelor și învățarea automată (ML). Acest ghid vă va ajuta să înțelegeți regresia liniară, modul în care este construită și tipurile, aplicațiile, beneficiile și dezavantajele acesteia.

Cuprins

• Ce este regresia liniară?
• Tipuri de regresie liniară
• Regresia liniară vs. regresia logistică
• Cum funcționează regresia liniară?
• Aplicații ale regresiei liniare
• Avantajele regresiei liniare în ML
• Dezavantajele regresiei liniare în ML

Ce este regresia liniară?

Regresia liniară este o metodă statistică utilizată în învățarea automată pentru a modela relația dintre o variabilă dependentă și una sau mai multe variabile independente. Modelează relațiile prin potrivirea unei ecuații liniare la datele observate, servind adesea ca punct de plecare pentru algoritmi mai complecși și este utilizat pe scară largă în analiza predictivă.

În esență, regresia liniară modelează relația dintre o variabilă dependentă (rezultatul pe care doriți să-l preziceți) și una sau mai multe variabile independente (funcțiile de intrare pe care le utilizați pentru predicție) prin găsirea liniei drepte care se potrivește cel mai bine printr-un set de puncte de date. Această linie, numitălinie de regresie, reprezintă relația dintre variabila dependentă (rezultatul pe care dorim să-l prezicem) și variabila(e) independentă (caracteristicile de intrare pe care le folosim pentru predicție). Ecuația pentru o dreaptă de regresie liniară simplă este definită astfel:

y = mx + c

unde y este variabila dependentă, x este variabila independentă, m este panta dreptei și c este intersecția cu y. Această ecuație oferă un model matematic pentru maparea intrărilor la ieșirile prezise, ​​cu scopul de a minimiza diferențele dintre valorile prezise și cele observate, cunoscute sub numele de reziduuri. Prin minimizarea acestor reziduuri, regresia liniară produce un model care reprezintă cel mai bine datele.

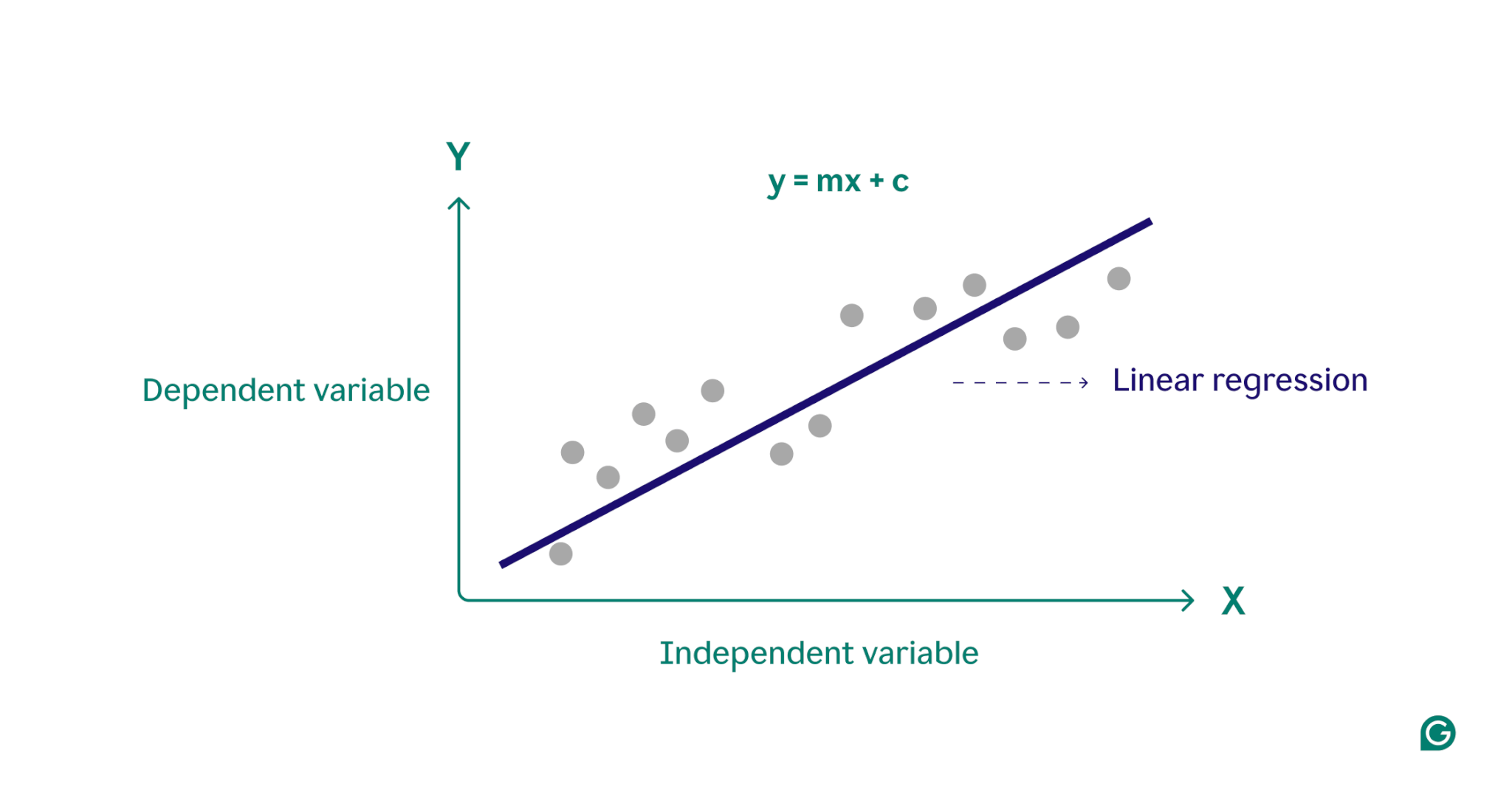
Din punct de vedere conceptual, regresia liniară poate fi vizualizată ca trasarea unei linii drepte prin puncte de pe un grafic pentru a determina dacă există o relație între acele puncte de date. Modelul de regresie liniară ideal pentru un set de puncte de date este linia care aproximează cel mai bine valorile fiecărui punct din setul de date.

Tipuri de regresie liniară

Există două tipuri principale de regresie liniară:regresie liniară simplășiregresie liniară multiplă.

Regresia liniară simplă

Regresia liniară simplă modelează relația dintre o singură variabilă independentă și o variabilă dependentă folosind o linie dreaptă. Ecuația pentru regresia liniară simplă este:

y = mx + c

unde y este variabila dependentă, x este variabila independentă, m este panta dreptei și c este intersecția cu y.

Această metodă este o modalitate simplă de a obține informații clare atunci când aveți de-a face cu scenarii cu o singură variabilă. Luați în considerare un medic care încearcă să înțeleagă modul în care înălțimea pacientului afectează greutatea. Prin trasarea fiecărei variabile pe un grafic și găsirea liniei care se potrivește cel mai bine folosind o regresie liniară simplă, medicul ar putea prezice greutatea pacientului doar pe înălțimea acestuia.

Regresie liniară multiplă

Regresia liniară multiplă extinde conceptul de regresie liniară simplă pentru a găzdui mai mult de o variabilă, permițând analiza modului în care factorii multipli influențează variabila dependentă. Ecuația pentru regresia liniară multiplă este:

y = b ₀ + b ₁ x ₁ + b ₂ x ₂ + … + b _n x _n

unde y este variabila dependentă, x ₁ , x ₂ , …, x _n sunt variabilele independente și b ₁ , b ₂ , …, b _n sunt coeficienții care descriu relația dintre fiecare variabilă independentă și variabila dependentă.

Ca exemplu, luați în considerare un agent imobiliar care dorește să estimeze prețurile caselor. Agentul ar putea folosi o regresie liniară simplă bazată pe o singură variabilă, cum ar fi dimensiunea casei sau codul poștal, dar acest model ar fi prea simplist, deoarece prețurile locuințelor sunt adesea determinate de o interacțiune complexă a mai multor factori. O regresie liniară multiplă, care încorporează variabile precum dimensiunea casei, cartierul și numărul de dormitoare, va oferi probabil un model de predicție mai precis.

Regresia liniară vs. regresia logistică

Regresia liniară este adesea confundată cu regresia logistică. În timp ce regresia liniară prezice rezultatele pe variabilecontinue, regresia logistică este utilizată atunci când variabila dependentă estecategorică, adesea binară (da sau nu). Variabilele categoriale definesc grupuri non-numerice cu un număr finit de categorii, cum ar fi grupa de vârstă sau metoda de plată. Variabilele continue, pe de altă parte, pot lua orice valoare numerică și sunt măsurabile. Exemple de variabile continue includ greutatea, prețul și temperatura zilnică.

Spre deosebire de funcția liniară utilizată în regresia liniară, regresia logistică modelează probabilitatea unui rezultat categoric folosind o curbă în formă de S numită funcție logistică. În exemplul clasificării binare, punctele de date care aparțin categoriei „da” se încadrează pe o parte a formei S, în timp ce punctele de date din categoria „nu” se încadrează pe cealaltă parte. Practic, regresia logistică poate fi folosită pentru a clasifica dacă un e-mail este sau nu spam sau pentru a prezice dacă un client va cumpăra sau nu un produs. În esență, regresia liniară este utilizată pentru prezicerea valorilor cantitative, în timp ce regresia logistică este utilizată pentru sarcinile de clasificare.

Cum funcționează regresia liniară?

Regresia liniară funcționează prin găsirea liniei care se potrivește cel mai bine printr-un set de puncte de date. Acest proces presupune:

1 Selectarea modelului:În primul pas, este selectată ecuația liniară adecvată pentru a descrie relația dintre variabilele dependente și independente.

2 Potrivirea modelului:În continuare, se utilizează o tehnică numită „Mărime pătrate obișnuite” (OLS) pentru a minimiza suma diferențelor pătrate dintre valorile observate și valorile prezise de model. Acest lucru se face prin ajustarea pantei și interceptarea liniei pentru a găsi cea mai bună potrivire. Scopul acestei metode este de a minimiza eroarea sau diferența dintre valorile prezise și cele reale. Acest proces de adaptare este o parte esențială a învățării automate supravegheate, în care modelul învață din datele de antrenament.

3 Evaluarea modelului:În pasul final, calitatea potrivirii este evaluată folosind metrici precum R-pătrat, care măsoară proporția varianței variabilei dependente care este previzibilă din variabilele independente. Cu alte cuvinte, R-pătrat măsoară cât de bine datele se potrivesc de fapt cu modelul de regresie.

Acest proces generează un model de învățare automată care poate fi apoi utilizat pentru a face predicții bazate pe date noi.

Aplicații ale regresiei liniare în ML

În învățarea automată, regresia liniară este un instrument utilizat în mod obișnuit pentru prezicerea rezultatelor și înțelegerea relațiilor dintre variabile din diferite domenii. Iată câteva exemple notabile ale aplicațiilor sale:

Prognoza cheltuielilor consumatorilor

Nivelurile veniturilor pot fi utilizate într-un model de regresie liniară pentru a prezice cheltuielile consumatorilor. Mai exact, regresia liniară multiplă ar putea include factori precum venitul istoric, vârsta și statutul de angajare pentru a oferi o analiză cuprinzătoare. Acest lucru poate ajuta economiștii să dezvolte politici economice bazate pe date și poate ajuta companiile să înțeleagă mai bine modelele de comportament ale consumatorilor.

Analiza impactului de marketing

Specialiștii în marketing pot folosi regresia liniară pentru a înțelege modul în care cheltuielile publicitare afectează veniturile din vânzări. Aplicând un model de regresie liniară datelor istorice, veniturile viitoare din vânzări pot fi prezise, ​​permițând marketerilor să-și optimizeze bugetele și strategiile de publicitate pentru un impact maxim.

Previziunea prețurilor acțiunilor

În lumea financiară, regresia liniară este una dintre numeroasele metode folosite pentru a prezice prețurile acțiunilor. Folosind date istorice de stoc și diverși indicatori economici, analiștii și investitorii pot construi mai multe modele de regresie liniară care îi ajută să ia decizii de investiții mai inteligente.

Prognoza condițiilor de mediu

În știința mediului, regresia liniară poate fi utilizată pentru a prognoza condițiile de mediu. De exemplu, diverși factori, cum ar fi volumul traficului, condițiile meteorologice și densitatea populației, pot ajuta la prezicerea nivelurilor de poluanți. Aceste modele de învățare automată pot fi apoi utilizate de factorii de decizie, oameni de știință și alte părți interesate pentru a înțelege și a atenua impactul diferitelor acțiuni asupra mediului.

Avantajele regresiei liniare în ML

Regresia liniară oferă mai multe avantaje care o fac o tehnică cheie în învățarea automată.

Simplu de utilizat și implementat

În comparație cu majoritatea instrumentelor și modelelor matematice, regresia liniară este ușor de înțeles și aplicat. Este deosebit de grozav ca punct de plecare pentru noii practicieni de învățare automată, oferind informații și experiență valoroase ca bază pentru algoritmi mai avansați.

Eficient din punct de vedere computațional

Modelele de învățare automată pot consuma multe resurse. Regresia liniară necesită o putere de calcul relativ scăzută în comparație cu mulți algoritmi și poate oferi în continuare informații predictive semnificative.

Rezultate interpretabile

Modelele statistice avansate, deși puternice, sunt adesea greu de interpretat. Cu un model simplu precum regresia liniară, relația dintre variabile este ușor de înțeles, iar impactul fiecărei variabile este clar indicat de coeficientul acesteia.

Fundație pentru tehnici avansate

Înțelegerea și implementarea regresiei liniare oferă o bază solidă pentru explorarea unor metode mai avansate de învățare automată. De exemplu, regresia polinomială se bazează pe regresia liniară pentru a descrie relații mai complexe, neliniare între variabile.

Dezavantajele regresiei liniare în ML

În timp ce regresia liniară este un instrument valoros în învățarea automată, are câteva limitări notabile. Înțelegerea acestor dezavantaje este esențială în selectarea instrumentului adecvat de învățare automată.

Presupunând o relație liniară

Modelul de regresie liniară presupune că relația dintre variabilele dependente și cele independente este liniară. În scenariile complexe din lumea reală, acest lucru poate să nu fie întotdeauna cazul. De exemplu, înălțimea unei persoane de-a lungul vieții este neliniară, creșterea rapidă care are loc în timpul copilăriei încetinind și oprindu-se la vârsta adultă. Deci, prognozarea înălțimii folosind regresia liniară ar putea duce la predicții inexacte.

Sensibilitate la valori aberante

Valorile aberante sunt puncte de date care se abat semnificativ de la majoritatea observațiilor dintr-un set de date. Dacă nu sunt tratate corespunzător, aceste puncte cu valori extreme pot denatura rezultatele, ducând la concluzii inexacte. În învățarea automată, această sensibilitate înseamnă că valorile aberante pot afecta în mod disproporționat acuratețea predictivă și fiabilitatea modelului.

Multicoliniaritate

În modelele de regresie liniară multiplă, variabilele independente foarte corelate pot distorsiona rezultatele, un fenomen cunoscut sub numele demulticoliniaritate. De exemplu, numărul de dormitoare dintr-o casă și dimensiunea acesteia ar putea fi foarte corelate, deoarece casele mai mari tind să aibă mai multe dormitoare. Acest lucru poate face dificilă determinarea impactului individual al variabilelor individuale asupra prețurilor locuințelor, ceea ce duce la rezultate nesigure.

Presupunând o răspândire constantă a erorii

Regresia liniară presupune că diferențele dintre valorile observate și cele prezise (distribuirea erorii) sunt aceleași pentru toate variabilele independente. Dacă acest lucru nu este adevărat, predicțiile generate de model pot fi nesigure. În învățarea automată supravegheată, nerezolvarea răspândirii erorilor poate determina modelul să genereze estimări părtinitoare și ineficiente, reducându-i eficacitatea generală.