Păduri aleatorii în învățarea automată: ce sunt și cum funcționează

Pădurile aleatorii sunt o tehnică puternică și versatilă în învățarea mașinilor (ML). Acest ghid vă va ajuta să înțelegeți pădurile aleatorii, modul în care funcționează și aplicațiile, beneficiile și provocările lor.

Cuprins

• Ce este o pădure aleatorie?
• Arbori de decizie vs. Forest Random: Care este diferența?
• Cum funcționează pădurile aleatorii
• Aplicații practice ale pădurilor aleatorii
• Avantajele pădurilor aleatorii
• Dezavantaje ale pădurilor aleatorii

Ce este o pădure aleatorie?

O pădure aleatorie este un algoritm de învățare automată care folosește mai mulți arbori de decizie pentru a face predicții. Este o metodă de învățare supravegheată concepută atât pentru sarcini de clasificare, cât și pentru regresie. Prin combinarea rezultatelor multor copaci, o pădure aleatorie îmbunătățește precizia, reduce supraîncărcarea și oferă predicții mai stabile în comparație cu un singur arbore de decizie.

Arbori de decizie vs. Forest Random: Care este diferența?

Deși pădurile aleatorii sunt construite pe arbori de decizie, cei doi algoritmi diferă semnificativ în structură și aplicare:

Copaci de decizie

Un arbore de decizie este format din trei componente principale: un nod rădăcină, noduri de decizie (noduri interne) și noduri ale frunzelor. Ca o diagramă de flux, procesul de decizie începe de la nodul rădăcină, trece prin nodurile de decizie pe baza condițiilor și se încheie la un nod de frunze reprezentând rezultatul. În timp ce copacii de decizie sunt ușor de interpretat și conceptualizați, sunt, de asemenea, predispuși la supra -a suprasolicitare, în special cu seturi de date complexe sau zgomotoase.

Păduri aleatorii

O pădure aleatorie este un ansamblu de arbori de decizie care își combină rezultatele pentru predicții îmbunătățite. Fiecare arbore este instruit pe un eșantion unic de bootstrap (un subset eșantionat aleatoriu al setului de date original cu înlocuire) și evaluează despărțirile de decizie folosind un subset de caracteristici selectat aleatoriu la fiecare nod. Această abordare, cunoscută sub numele de Bagging cu caracteristici, introduce diversitatea în rândul copacilor. Prin agregarea predicțiilor - folosind votarea majorității pentru clasificare sau medii pentru regresie - pădurile de random produc rezultate mai precise și stabile decât orice arbore de decizie unic din ansamblu.

Cum funcționează pădurile aleatorii

Pădurile aleatorii operează prin combinarea multiplă a arborilor de decizie pentru a crea un model de predicție robust și precis.

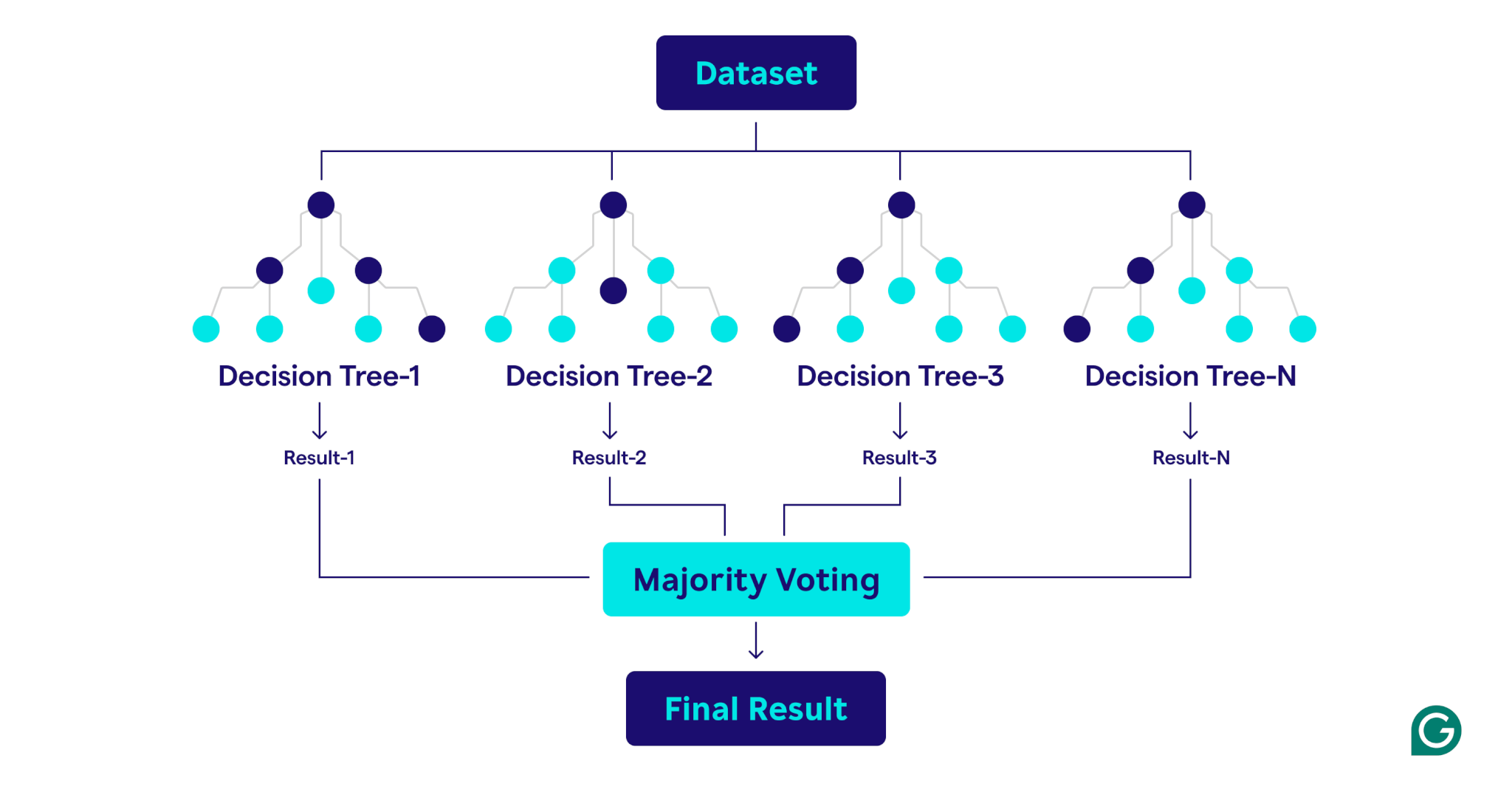
Iată o explicație pas cu pas a procesului:

1. Setarea hiperparametrelor

Primul pas este definirea hiperparametrelor modelului. Acestea includ:

• Numărul de copaci:Determină dimensiunea pădurii
• Adâncime maximă pentru fiecare copac:controlează cât de adânc poate crește fiecare arbore de decizie
• Numărul de caracteristici luate în considerare la fiecare divizare:limitează numărul de caracteristici evaluate la crearea de despărțiri

Aceste hiperparametre permit reglarea fină a complexității modelului și optimizarea performanței pentru seturi de date specifice.

2. Eșantionarea bootstrap

Odată ce hiperparametrele sunt stabilite, procesul de instruire începe cu eșantionarea cu bootstrap. Aceasta implică:

• Punctele de date din setul de date original sunt selectate aleatoriu pentru a crea seturi de date de instruire (eșantioane de bootstrap) pentru fiecare arbore de decizie.
• Fiecare eșantion de bootstrap este de obicei aproximativ două treimi din dimensiunea setului de date original, cu unele puncte de date repetate, iar altele excluse.
• Restul treilea din punctele de date, care nu sunt incluse în eșantionul de bootstrap, este denumit date din afara bagului (OOB).

3. Construirea copacilor de decizie

Fiecare arbore de decizie din pădurea aleatorie este instruit pe eșantionul său de bootstrap corespunzător folosind un proces unic:

• Bătăile de caracteristici:la fiecare despărțire, este selectat un subset aleatoriu de caracteristici, asigurând diversitatea dintre copaci.
• Divizarea nodului:cea mai bună caracteristică din subset este utilizată pentru a împărți nodul:
  • Pentru sarcini de clasificare, criterii precum impuritatea Gini (o măsură a cât de des ar fi clasificat incorect un element ales la întâmplare dacă ar fi etichetat aleatoriu în funcție de distribuția etichetelor de clasă în nod), măsurați cât de bine despărțirea despărțirii claselor.
  • Pentru sarcinile de regresie, tehnici precum reducerea variației (metodă care măsoară cât de mult divizarea unui nod scade variația valorilor țintă, ceea ce duce la predicții mai precise) evaluează cât de mult se reduce divizarea erorii de predicție.
• Arborele crește recursiv până când îndeplinește condițiile de oprire, cum ar fi o adâncime maximă sau un număr minim de puncte de date pe nod.

4. Evaluarea performanței

Pe măsură ce fiecare arbore este construit, performanța modelului este estimată folosind datele OOB:

• Estimarea erorilor OOB oferă o măsură imparțială a performanței modelului, eliminând necesitatea unui set de date de validare separat.
• Prin agregarea predicțiilor din partea tuturor copacilor, pădurea aleatorie obține o precizie îmbunătățită și reduce supra -comisionarea în comparație cu arborii de decizie individuali.

Aplicații practice ale pădurilor aleatorii

La fel ca arborii de decizie pe care sunt construiți, pădurile aleatorii pot fi aplicate problemelor de clasificare și regresie într -o mare varietate de sectoare, cum ar fi asistența medicală și finanțele.

Clasificarea afecțiunilor pacientului

În asistență medicală, pădurile aleatorii sunt utilizate pentru a clasifica condițiile pacientului pe baza informațiilor precum istoricul medical, demografia și rezultatele testelor. De exemplu, pentru a prezice dacă un pacient este probabil să dezvolte o afecțiune specifică precum diabetul, fiecare arbore de decizie clasifică pacientul ca fiind la risc sau nu pe baza datelor relevante, iar pădurea aleatorie face determinarea finală pe baza unui vot majoritar. Această abordare înseamnă că pădurile aleatorii sunt deosebit de potrivite pentru seturile de date complexe, bogate în caracteristici, găsite în asistența medicală.

Prezicerea valorilor implicite ale împrumutului

Băncile și instituțiile financiare majore folosesc pe scară largă păduri aleatorii pentru a determina eligibilitatea împrumutului și pentru a înțelege mai bine riscul. Modelul folosește factori precum venitul și scorul de credit pentru a determina riscul. Deoarece riscul este măsurat ca o valoare numerică continuă, pădurea aleatorie efectuează regresie în loc de clasificare. Fiecare arbore de decizie, instruit pe probe ușor diferite de bootstrap, produce un scor de risc prevăzut. Apoi, pădurea aleatorie are în medie toate predicțiile individuale, ceea ce duce la o estimare robustă, holistică a riscului.

Prezicerea pierderii clienților

În marketing, pădurile aleatorii sunt adesea folosite pentru a prezice probabilitatea ca un client să întrerupă utilizarea unui produs sau serviciu. Aceasta implică analizarea modelelor de comportament al clienților, cum ar fi frecvența de cumpărare și interacțiunile cu serviciul pentru clienți. Prin identificarea acestor modele, pădurile aleatorii pot clasifica clienții cu risc de a pleca. Cu aceste informații, companiile pot lua măsuri proactive, bazate pe date pentru a reține clienții, cum ar fi oferirea de programe de loialitate sau promoții vizate.

Prezicerea prețurilor imobiliare

Pădurile aleatorii pot fi utilizate pentru a prezice prețurile imobiliare, ceea ce este o sarcină de regresie. Pentru a face predicția, pădurea aleatorie folosește date istorice care includ factori precum locația geografică, materialul pătrat și vânzările recente în zonă. Procesul de medie a pădurii aleatorii are ca rezultat o predicție a prețurilor mai fiabilă și mai stabilă decât cea a unui arbore de decizie individual, care este util pe piețele imobiliare extrem de volatile.

Avantajele pădurilor aleatorii

Pădurile aleatorii oferă numeroase avantaje, inclusiv precizia, robustetea, versatilitatea și capacitatea de a estima importanța caracteristică.

Precizie și robustete

Pădurile aleatorii sunt mai exacte și mai robuste decât arborii de decizie individuali. Acest lucru se realizează prin combinarea rezultatelor mai multor arbori de decizie instruiți pe diferite eșantioane de bootstrap ale setului de date original. Diversitatea rezultată înseamnă că pădurile aleatorii sunt mai puțin predispuse la suprasolicitare decât copacii de decizie individuali. Această abordare a ansamblului înseamnă că pădurile aleatorii sunt bune în gestionarea datelor zgomotoase, chiar și în seturi de date complexe.

Versatilitate

Ca și arborii de decizie pe care sunt construiți, pădurile aleatorii sunt extrem de versatile. Ele pot gestiona atât sarcinile de regresie, cât și de clasificare, ceea ce le face aplicabile unei game largi de probleme. Pădurile aleatorii funcționează bine, de asemenea, cu seturi de date mari, bogate în caracteristici, și pot gestiona atât date numerice, cât și categorice.

Importanță caracteristică

Pădurile aleatorii au o capacitate încorporată de a estima importanța unor caracteristici particulare. Ca parte a procesului de antrenament, pădurile aleatorii produc un scor care măsoară cât de mult se schimbă precizia modelului dacă o anumită caracteristică este eliminată. Prin media scorurilor pentru fiecare caracteristică, pădurile aleatorii pot oferi o măsură cuantificabilă a importanței caracteristicii. Caracteristici mai puțin importante pot fi apoi eliminate pentru a crea copaci și păduri mai eficiente.

Dezavantaje ale pădurilor aleatorii

În timp ce pădurile aleatorii oferă multe beneficii, acestea sunt mai greu de interpretat și mai costisitoare pentru a se antrena decât un singur arbore de decizie și pot produce predicții mai lent decât alte modele.

Complexitate

În timp ce pădurile aleatorii și arborii de decizie au multe în comun, pădurile aleatorii sunt mai greu de interpretat și vizualizat. Această complexitate apare deoarece pădurile aleatorii folosesc sute sau mii de arbori de decizie. Natura „cutiei negre” a pădurilor aleatorii este un dezavantaj serios atunci când explicabilitatea modelului este o cerință.

Cost de calcul

Instruirea a sute sau mii de arbori de decizie necesită mult mai multă putere de procesare și memorie decât formarea unui singur arbore de decizie. Când sunt implicate seturi de date mari, costul de calcul poate fi și mai mare. Această cerință mare de resurse poate duce la costuri monetare mai mari și timpi de pregătire mai lungi. Drept urmare, este posibil ca pădurile aleatorii să nu fie practice în scenarii precum calculul de margine, unde atât puterea de calcul, cât și memoria sunt rare. Cu toate acestea, pădurile aleatorii pot fi paralelizate, ceea ce poate ajuta la reducerea costului de calcul.

Timp de predicție mai lent

Procesul de predicție al unei păduri aleatorii implică traversarea fiecărui copac din pădure și agregarea producțiilor lor, care este în mod mai lent mai lent decât utilizarea unui singur model. Acest proces poate duce la timp de predicție mai lent decât modele mai simple, cum ar fi regresia logistică sau rețelele neuronale, în special pentru pădurile mari care conțin copaci adânci. Pentru cazuri de utilizare în care timpul este esențial, cum ar fi tranzacționarea de înaltă frecvență sau vehiculele autonome, această întârziere poate fi prohibitivă.