Что такое дерево решений в машинном обучении?
Опубликовано: 2024-08-14Деревья решений — один из наиболее распространенных инструментов в наборе инструментов машинного обучения аналитика данных. В этом руководстве вы узнаете, что такое деревья решений, как они строятся, различные приложения, преимущества и многое другое.
Оглавление
- Что такое дерево решений?
- Терминология дерева решений
- Типы деревьев решений
- Как работают деревья решений
- Приложения
- Преимущества
- Недостатки
Что такое дерево решений?
В машинном обучении (МО) дерево решений — это контролируемый алгоритм обучения, напоминающий блок-схему или диаграмму решений. В отличие от многих других алгоритмов обучения с учителем, деревья решений можно использовать как для задач классификации, так и для регрессии. Специалисты по данным и аналитики часто используют деревья решений при исследовании новых наборов данных, поскольку их легко построить и интерпретировать. Кроме того, деревья решений могут помочь определить важные функции данных, которые могут быть полезны при применении более сложных алгоритмов машинного обучения.
Терминология дерева решений
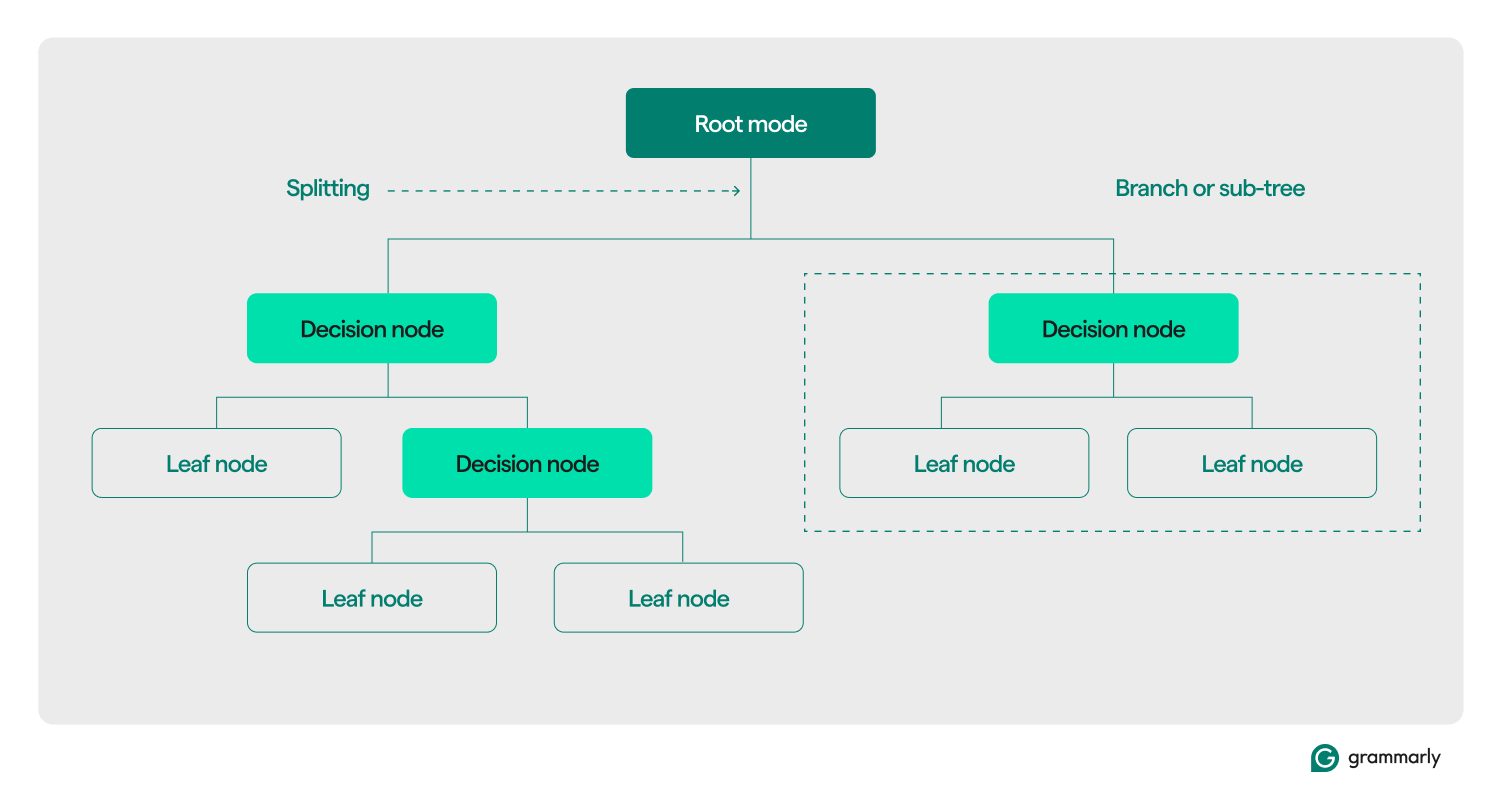
Структурно дерево решений обычно состоит из трех компонентов: корневого узла, конечных узлов и узлов принятия решений (или внутренних). Подобно блок-схемам или деревьям в других областях, решения в дереве обычно движутся в одном направлении (вниз или вверх), начиная с корневого узла, проходя через некоторые узлы принятия решений и заканчивая конкретным листовым узлом. Каждый листовой узел соединяет подмножество обучающих данных с меткой. Дерево собирается в процессе обучения и оптимизации машинного обучения, и после построения его можно применять к различным наборам данных.
Вот более глубокое погружение в остальную терминологию:
- Корневой узел:узел, содержащий первый из серии вопросов, которые дерево решений задаст о данных. Узел будет подключен по крайней мере к одному (но обычно к двум или более) узлам принятия решений или листовым узлам.
- Узлы принятия решений (или внутренние узлы):дополнительные узлы, содержащие вопросы. Узел принятия решения будет содержать ровно один вопрос о данных и направлять поток данных одному из своих дочерних элементов на основе ответа.
- Дочерние узлы:один или несколько узлов, на которые указывает корень или узел принятия решений. Они представляют собой список следующих вариантов, которые может принять процесс принятия решений при анализе данных.
- Листовые узлы (или терминальные узлы):узлы, указывающие на завершение процесса принятия решения. Как только процесс принятия решения достигнет конечного узла, он вернет значения из конечного узла в качестве выходных данных.
- Метка (класс, категория):Обычно это строка, связанная конечным узлом с некоторыми обучающими данными. Например, лист может связать метку «Довольный клиент» с набором конкретных клиентов, которым был представлен алгоритм обучения ML дерева решений.
- Ветвь (или поддерево):это набор узлов, состоящий из узла решения в любой точке дерева вместе со всеми его дочерними элементами и их дочерними элементами, вплоть до конечных узлов.
- Обрезка:операция оптимизации, обычно выполняемая с деревом, чтобы уменьшить его размер и ускорить возврат результатов. Под обрезкой обычно подразумевается «пост-обрезка», которая включает в себя алгоритмическое удаление узлов или ветвей после того, как процесс обучения ML построил дерево. «Предварительная обрезка» означает установку произвольного предела глубины или размера дерева решений во время обучения. Оба процесса обеспечивают максимальную сложность дерева решений, обычно измеряемую его максимальной глубиной или высотой. Менее распространенные оптимизации включают ограничение максимального количества узлов принятия решений или конечных узлов.
- Разделение:основной шаг преобразования, выполняемый в дереве решений во время обучения. Он предполагает разделение корневого узла или узла принятия решений на два или более подузлов.
- Классификация:алгоритм машинного обучения, который пытается выяснить, какой (из постоянного и дискретного списка классов, категорий или меток) наиболее вероятно применим к фрагменту данных. Он может попытаться ответить на такие вопросы, как «В какой день недели лучше всего забронировать рейс?» Подробнее о классификации ниже.
- Регрессия:алгоритм машинного обучения, который пытается предсказать непрерывное значение, которое не всегда может иметь границы. Он может попытаться ответить (или предсказать ответ) на такие вопросы, как «Сколько людей, скорее всего, забронируют рейс в следующий вторник?» Мы поговорим подробнее о деревьях регрессии в следующем разделе.
Типы деревьев решений
Деревья решений обычно группируются в две категории: деревья классификации и деревья регрессии. Можно построить конкретное дерево, применимое к классификации, регрессии или к обоим вариантам использования. В большинстве современных деревьев решений используется алгоритм CART (деревья классификации и регрессии), который может выполнять оба типа задач.
Деревья классификации
Деревья классификации, наиболее распространенный тип дерева решений, пытаются решить проблему классификации. Из списка возможных ответов на вопрос (часто таких простых, как «да» или «нет») дерево классификации выберет наиболее вероятный ответ после того, как будет задано несколько вопросов о представленных ему данных. Обычно они реализуются в виде двоичных деревьев, то есть каждый узел принятия решений имеет ровно два дочерних элемента.
Деревья классификации могут попытаться ответить на вопросы с несколькими вариантами ответов, например: «Удовлетворен ли этот клиент?» или «Какой физический магазин скорее всего посетит этот клиент?» или «Будет ли завтра хороший день, чтобы пойти на поле для гольфа?»
Два наиболее распространенных метода измерения качества дерева классификации основаны на приросте информации и энтропии:
- Получение информации.Эффективность дерева повышается, когда оно задает меньше вопросов, прежде чем получить ответ. Прирост информации измеряет, насколько «быстро» дерево может получить ответ, оценивая, насколько больше информации будет получено о фрагменте данных в каждом узле принятия решения. Он оценивает, задаются ли в дереве первыми самые важные и полезные вопросы.
- Энтропия:точность имеет решающее значение для меток дерева решений. Метрики энтропии измеряют эту точность путем оценки меток, созданных деревом. Они оценивают, как часто случайному фрагменту данных присваивается неправильная метка, а также сходство между всеми фрагментами обучающих данных, получившими одну и ту же метку.
Более продвинутые измерения качества дерева включаютиндекс Джини,коэффициент усиления,оценки хи-квадрати различные измерения для уменьшения дисперсии.
Деревья регрессии
Деревья регрессии обычно используются в регрессионном анализе для расширенного статистического анализа или для прогнозирования данных из непрерывного, потенциально неограниченного диапазона. Учитывая диапазон непрерывных вариантов (например, от нуля до бесконечности в шкале действительных чисел), дерево регрессии пытается предсказать наиболее вероятное совпадение для данного фрагмента данных после постановки ряда вопросов. Каждый вопрос сужает потенциальный диапазон ответов. Например, дерево регрессии можно использовать для прогнозирования кредитного рейтинга, дохода от направления бизнеса или количества взаимодействий с маркетинговым видео.
Точность деревьев регрессии обычно оценивается с использованием таких показателей, каксреднеквадратическая ошибкаилисредняя абсолютная ошибка, которые рассчитывают, насколько далеко конкретный набор прогнозов сравнивается с фактическими значениями.
Как работают деревья решений
В качестве примера обучения с учителем деревья решений основаны на хорошо отформатированных данных для обучения. Исходные данные обычно содержат список значений, которые модель должна научиться прогнозировать или классифицировать. К каждому значению должна быть прикреплена метка и список связанных функций — свойств, которые модель должна научиться связывать с меткой.

Строительство или обучение
В процессе обучения узлы решений в дереве решений рекурсивно разбиваются на более конкретные узлы в соответствии с одним или несколькими алгоритмами обучения. Описание процесса на человеческом уровне может выглядеть так:
- Начните с корневого узла,подключенного ко всему обучающему набору.
- Разделите корневой узел:используя статистический подход, назначьте решение корневому узлу на основе одной из функций данных и распределите обучающие данные как минимум на два отдельных конечных узла, подключенных как дочерние к корню.
- Рекурсивно примените второй шагк каждому из дочерних элементов, превратив их из конечных узлов в узлы принятия решений. Остановитесь, когда будет достигнут некоторый предел (например, высота/глубина дерева, мера качества дочерних элементов на каждом листе в каждом узле и т. д.) или если у вас закончились данные (т. е. каждый лист содержит данные). точки, относящиеся ровно к одной метке).
Решение о том, какие функции учитывать на каждом узле, различается для сценариев использования классификации, регрессии и комбинированной классификации и регрессии. Для каждого сценария существует множество алгоритмов на выбор. Типичные алгоритмы включают в себя:
- ID3 (классификация):оптимизирует энтропию и получение информации.
- C4.5 (классификация):более сложная версия ID3, добавляющая нормализацию к получению информации.
- CART (классификация/регрессия): «Дерево классификации и регрессии»; жадный алгоритм, который оптимизирует минимальную примесь в наборах результатов
- CHAID (классификация/регрессия): «автоматическое обнаружение взаимодействия по хи-квадрату»; использует измерения хи-квадрат вместо энтропии и прироста информации
- MARS (классификация/регрессия): использует кусочно-линейные аппроксимации для выявления нелинейностей.
Распространенным режимом обучения является случайный лес. Случайный лес или случайный лес решений — это система, которая строит множество связанных деревьев решений. Несколько версий дерева могут обучаться параллельно, используя комбинации алгоритмов обучения. На основе различных измерений качества деревьев для получения ответа будет использоваться подмножество этих деревьев. В случаях использования классификации в качестве ответа возвращается класс, выбранный наибольшим количеством деревьев. В случаях использования регрессии ответ агрегируется, обычно как среднее или среднее предсказание отдельных деревьев.
Оценка и использование деревьев решений
После построения дерева решений оно может классифицировать новые данные или прогнозировать значения для конкретного варианта использования. Важно сохранять показатели производительности дерева и использовать их для оценки точности и частоты ошибок. Если модель слишком сильно отклоняется от ожидаемой производительности, возможно, пришло время переобучить ее на новых данных или найти другие системы машинного обучения, которые можно применить к этому варианту использования.
Применение деревьев решений в машинном обучении
Деревья решений имеют широкий спектр применения в различных областях. Вот несколько примеров, иллюстрирующих их универсальность:
Информированное личное принятие решений
Человек может отслеживать данные, скажем, о ресторанах, которые он посещал. Они могут отслеживать любые важные детали, такие как время в пути, время ожидания, предлагаемая кухня, часы работы, средний балл по отзывам, стоимость и последнее посещение, а также оценка удовлетворенности посещением этого ресторана человеком. На основе этих данных можно обучить дерево решений, чтобы спрогнозировать вероятный показатель удовлетворенности нового ресторана.
Рассчитать вероятности поведения клиентов
Системы поддержки клиентов могут использовать деревья решений для прогнозирования или классификации удовлетворенности клиентов. Дерево решений можно обучить прогнозированию удовлетворенности клиентов на основе различных факторов, например, обращался ли клиент в службу поддержки или совершил повторную покупку, или на основе действий, выполненных в приложении. Кроме того, он может включать результаты опросов удовлетворенности или другие отзывы клиентов.
Помощь в принятии бизнес-решений
Для определенных бизнес-решений, основанных на большом количестве исторических данных, дерево решений может предоставить оценки или прогнозы для следующих шагов. Например, компания, которая собирает демографическую и географическую информацию о своих клиентах, может обучить дерево решений для оценки того, какие новые географические местоположения могут быть прибыльными, а каких следует избегать. Деревья решений также могут помочь определить наилучшие границы классификации для существующих демографических данных, например, определить возрастные диапазоны, которые следует учитывать отдельно при группировке клиентов.
Выбор функций для расширенного машинного обучения и других вариантов использования
Древовидные структуры решений легко читаются и понятны человеку. После построения дерева можно определить, какие функции наиболее актуальны для набора данных и в каком порядке. Эта информация может помочь в разработке более сложных систем машинного обучения или алгоритмов принятия решений. Например, если бизнес узнает из дерева решений, что клиенты отдают приоритет стоимости продукта превыше всего, он может сосредоточить внимание на более сложных системах машинного обучения на этом понимании или игнорировать затраты при изучении более тонких функций.
Преимущества деревьев решений в ML
Деревья решений обладают рядом существенных преимуществ, которые делают их популярным выбором в приложениях машинного обучения. Вот некоторые ключевые преимущества:
Быстро и легко построить
Деревья решений — один из наиболее зрелых и хорошо понятных алгоритмов машинного обучения. Они не требуют особо сложных расчетов и могут быть построены быстро и легко. Если необходимая информация легко доступна, дерево решений — это простой первый шаг при рассмотрении решения проблемы с помощью машинного обучения.
Легко понять людям
Результаты деревьев решений особенно легко читать и интерпретировать. Графическое представление дерева решений не зависит от глубокого понимания статистики. Таким образом, деревья решений и их представления могут использоваться для интерпретации, объяснения и поддержки результатов более сложного анализа. Деревья решений отлично подходят для поиска и выделения некоторых высокоуровневых свойств данного набора данных.
Требуется минимальная обработка данных
Деревья решений можно так же легко построить на основе неполных данных или данных с включенными выбросами. Учитывая данные, украшенные интересными функциями, алгоритмы дерева решений, как правило, не подвергаются такому сильному влиянию, как другие алгоритмы ML, если им подаются данные, которые не были предварительно обработаны.
Недостатки деревьев решений в ML
Хотя деревья решений предлагают множество преимуществ, они также имеют ряд недостатков:
Подвержен переоснащению
Деревья решений склонны к переоснащению, которое происходит, когда модель изучает шум и детали в обучающих данных, что снижает ее производительность на новых данных. Например, если обучающие данные неполны или разрежены, небольшие изменения в данных могут привести к существенному изменению древовидных структур. Продвинутые методы, такие как обрезка или установка максимальной глубины, могут улучшить поведение дерева. На практике деревья решений часто требуют обновления новой информацией, что может существенно изменить их структуру.
Плохая масштабируемость
Помимо склонности к переобучению, деревья решений борются с более сложными проблемами, требующими значительно больше данных. По сравнению с другими алгоритмами время обучения деревьев решений быстро увеличивается по мере роста объемов данных. Для больших наборов данных, которые могут иметь важные свойства высокого уровня, которые необходимо обнаружить, деревья решений не подходят.
Не так эффективно для случаев регрессии или непрерывного использования.
Деревья решений не очень хорошо изучают сложные распределения данных. Они разделяют пространство признаков по линиям, которые легко понять, но математически просты. Для сложных задач, где важны выбросы, регрессия и сценарии непрерывного использования, это часто приводит к гораздо более низкой производительности, чем другие модели и методы ML.
