Что такое линейная регрессия в машинном обучении?
Опубликовано: 2024-09-06Линейная регрессия — это основополагающий метод анализа данных и машинного обучения (ML). Это руководство поможет вам понять линейную регрессию, как она устроена, а также ее типы, приложения, преимущества и недостатки.
Оглавление
- Что такое линейная регрессия?
- Виды линейной регрессии
- Линейная регрессия против логистической регрессии
- Как работает линейная регрессия?
- Применение линейной регрессии
- Преимущества линейной регрессии в ML
- Недостатки линейной регрессии в ML
Что такое линейная регрессия?
Линейная регрессия — это статистический метод, используемый в машинном обучении для моделирования взаимосвязи между зависимой переменной и одной или несколькими независимыми переменными. Он моделирует взаимосвязи путем подгонки линейного уравнения к наблюдаемым данным, часто служит отправной точкой для более сложных алгоритмов и широко используется в прогнозном анализе.
По сути, линейная регрессия моделирует взаимосвязь между зависимой переменной (результатом, который вы хотите спрогнозировать) и одной или несколькими независимыми переменными (входными признаками, которые вы используете для прогнозирования), находя наиболее подходящую прямую линию через набор точек данных. Эта линия, называемаялинией регрессии, представляет взаимосвязь между зависимой переменной (результат, который мы хотим спрогнозировать) и независимой переменной(ями) (входные признаки, которые мы используем для прогнозирования). Уравнение для простой линии линейной регрессии определяется как:
у = мх + с
где y — зависимая переменная, x — независимая переменная, m — наклон линии, а c — точка пересечения оси y. Это уравнение представляет собой математическую модель для сопоставления входных данных с прогнозируемыми выходными данными с целью минимизации различий между прогнозируемыми и наблюдаемыми значениями, известных как остатки. Минимизируя эти остатки, линейная регрессия создает модель, которая лучше всего представляет данные.
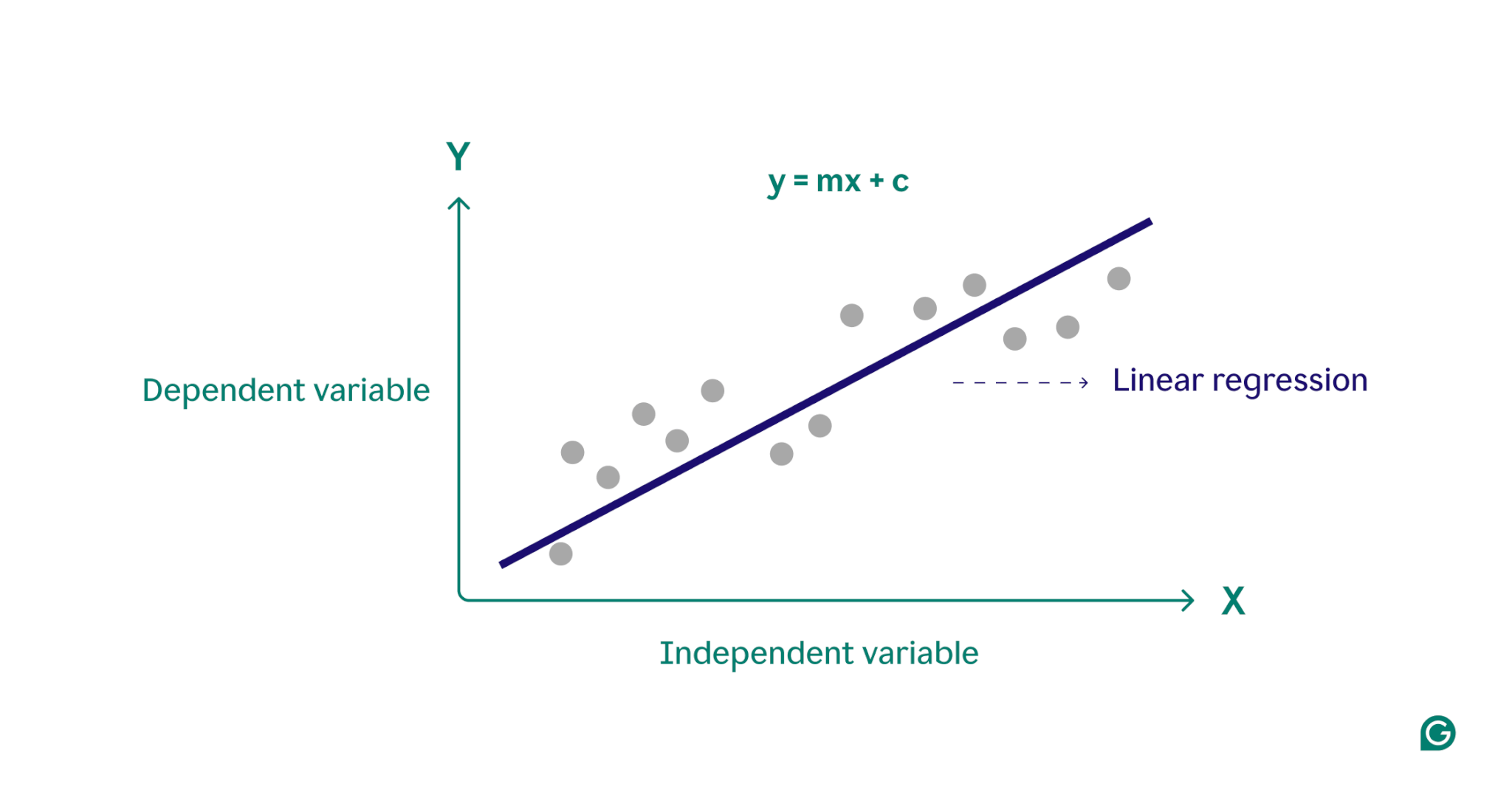
Концептуально линейную регрессию можно представить как проведение прямой линии через точки на графике, чтобы определить, существует ли связь между этими точками данных. Идеальная модель линейной регрессии для набора точек данных — это линия, которая лучше всего аппроксимирует значения каждой точки в наборе данных.
Виды линейной регрессии
Существует два основных типа линейной регрессии:простая линейная регрессияимножественная линейная регрессия.
Простая линейная регрессия
Простая линейная регрессия моделирует взаимосвязь между одной независимой переменной и зависимой переменной, используя прямую линию. Уравнение простой линейной регрессии:
у = мх + с
где y — зависимая переменная, x — независимая переменная, m — наклон линии, а c — точка пересечения оси y.
Этот метод представляет собой простой способ получить четкое представление о сценариях с одной переменной. Представьте себе врача, пытающегося понять, как рост пациента влияет на вес. Поместив каждую переменную на график и найдя наиболее подходящую линию с помощью простой линейной регрессии, врач мог предсказать вес пациента, основываясь только на его росте.
Множественная линейная регрессия
Множественная линейная регрессия расширяет концепцию простой линейной регрессии, позволяя учитывать более одной переменной, позволяя анализировать, как несколько факторов влияют на зависимую переменную. Уравнение для множественной линейной регрессии:
y = b 0 + b 1 x 1 + b 2 x 2 + … + b n x n
где y – зависимая переменная, x 1 , x 2 , …, x n – независимые переменные, а b 1 , b 2 , …, bn – коэффициенты, описывающие связь между каждой независимой переменной и зависимой переменной.
В качестве примера рассмотрим агента по недвижимости, который хочет оценить цены на жилье. Агент мог бы использовать простую линейную регрессию, основанную на одной переменной, например, размере дома или почтовом индексе, но эта модель была бы слишком упрощенной, поскольку цены на жилье часто определяются сложным взаимодействием множества факторов. Множественная линейная регрессия, включающая такие переменные, как размер дома, район и количество спален, вероятно, обеспечит более точную модель прогнозирования.
Линейная регрессия против логистической регрессии
Линейную регрессию часто путают с логистической регрессией. В то время как линейная регрессия предсказывает результаты понепрерывнымпеременным, логистическая регрессия используется, когда зависимая переменная являетсякатегориальной, часто бинарной (да или нет). Категориальные переменные определяют нечисловые группы с конечным числом категорий, например возрастную группу или способ оплаты. С другой стороны, непрерывные переменные могут принимать любое числовое значение и измеримы. Примеры непрерывных переменных включают вес, цену и дневную температуру.
В отличие от линейной функции, используемой в линейной регрессии, логистическая регрессия моделирует вероятность категориального результата с помощью S-образной кривой, называемой логистической функцией. В примере бинарной классификации точки данных, относящиеся к категории «да», попадают на одну сторону S-образной формы, а точки данных из категории «нет» — на другую сторону. Практически говоря, логистическую регрессию можно использовать для классификации того, является ли электронное письмо спамом или нет, или для прогнозирования, купит ли клиент продукт или нет. По сути, линейная регрессия используется для прогнозирования количественных значений, тогда как логистическая регрессия используется для задач классификации.
Как работает линейная регрессия?
Линейная регрессия работает путем поиска наиболее подходящей линии через набор точек данных. Этот процесс включает в себя:
1 Выбор модели.На первом этапе выбирается подходящее линейное уравнение для описания взаимосвязи между зависимыми и независимыми переменными.

2. Подгонка модели.Затем используется метод под названием «обычные наименьшие квадраты» (OLS) для минимизации суммы квадратов разностей между наблюдаемыми значениями и значениями, предсказанными моделью. Это делается путем регулировки наклона и точки пересечения линии, чтобы найти наилучшее соответствие. Целью этого метода является минимизация ошибки или разницы между прогнозируемыми и фактическими значениями. Этот процесс подгонки является основной частью контролируемого машинного обучения, в котором модель учится на обучающих данных.
3 Оценка модели.На последнем этапе качество соответствия оценивается с использованием таких показателей, как R-квадрат, который измеряет долю дисперсии зависимой переменной, предсказуемую на основе независимых переменных. Другими словами, R-квадрат измеряет, насколько хорошо данные фактически соответствуют модели регрессии.
В результате этого процесса создается модель машинного обучения, которую затем можно использовать для прогнозирования на основе новых данных.
Применение линейной регрессии в машинном обучении
В машинном обучении линейная регрессия является широко используемым инструментом для прогнозирования результатов и понимания взаимосвязей между переменными в различных областях. Вот несколько ярких примеров его применения:
Прогнозирование потребительских расходов
Уровни доходов можно использовать в модели линейной регрессии для прогнозирования потребительских расходов. В частности, множественная линейная регрессия может включать такие факторы, как исторический доход, возраст и статус занятости, чтобы обеспечить комплексный анализ. Это может помочь экономистам в разработке экономической политики, основанной на данных, а также помочь предприятиям лучше понять модели поведения потребителей.
Анализ маркетингового воздействия
Маркетологи могут использовать линейную регрессию, чтобы понять, как расходы на рекламу влияют на доход от продаж. Применяя модель линейной регрессии к историческим данным, можно прогнозировать будущие доходы от продаж, что позволяет маркетологам оптимизировать свои бюджеты и рекламные стратегии для достижения максимального эффекта.
Прогнозирование цен на акции
В мире финансов линейная регрессия — один из многих методов, используемых для прогнозирования цен на акции. Используя исторические данные о фондовых рынках и различные экономические показатели, аналитики и инвесторы могут построить несколько моделей линейной регрессии, которые помогут им принимать более разумные инвестиционные решения.
Прогнозирование условий окружающей среды
В науке об окружающей среде линейная регрессия может использоваться для прогнозирования условий окружающей среды. Например, различные факторы, такие как интенсивность движения, погодные условия и плотность населения, могут помочь предсказать уровни загрязнения. Эти модели машинного обучения затем могут использоваться политиками, учеными и другими заинтересованными сторонами для понимания и смягчения воздействия различных действий на окружающую среду.
Преимущества линейной регрессии в ML
Линейная регрессия предлагает несколько преимуществ, которые делают ее ключевым методом машинного обучения.
Простота в использовании и реализации
По сравнению с большинством математических инструментов и моделей, линейную регрессию легко понять и применить. Он особенно хорош в качестве отправной точки для новых практиков машинного обучения, предоставляя ценную информацию и опыт в качестве основы для более совершенных алгоритмов.
Вычислительная эффективность
Модели машинного обучения могут быть ресурсоемкими. Линейная регрессия требует относительно небольшой вычислительной мощности по сравнению со многими алгоритмами и при этом может обеспечить значимую прогностическую информацию.
Интерпретируемые результаты
Усовершенствованные статистические модели, хотя и эффективны, часто их трудно интерпретировать. С помощью такой простой модели, как линейная регрессия, взаимосвязь между переменными легко понять, а влияние каждой переменной четко обозначается ее коэффициентом.
Фонд передовых технологий
Понимание и реализация линейной регрессии предлагает прочную основу для изучения более совершенных методов машинного обучения. Например, полиномиальная регрессия основана на линейной регрессии для описания более сложных нелинейных связей между переменными.
Недостатки линейной регрессии в ML
Хотя линейная регрессия является ценным инструментом машинного обучения, она имеет несколько заметных ограничений. Понимание этих недостатков имеет решающее значение при выборе подходящего инструмента машинного обучения.
Предполагая линейную зависимость
Модель линейной регрессии предполагает, что связь между зависимыми и независимыми переменными линейна. В сложных реальных сценариях это не всегда так. Например, рост человека в течение жизни нелинейен: быстрый рост, происходящий в детстве, замедляется и прекращается во взрослом возрасте. Таким образом, прогнозирование высоты с использованием линейной регрессии может привести к неточным прогнозам.
Чувствительность к выбросам
Выбросы — это точки данных, которые значительно отклоняются от большинства наблюдений в наборе данных. Если с ними не обращаться должным образом, эти экстремальные значения могут исказить результаты, что приведет к неверным выводам. В машинном обучении эта чувствительность означает, что выбросы могут непропорционально повлиять на точность прогнозирования и надежность модели.
Мультиколлинеарность
В моделях множественной линейной регрессии сильно коррелированные независимые переменные могут искажать результаты — явление, известное какмультиколлинеарность. Например, количество спален в доме и его размер могут сильно коррелировать, поскольку в больших домах обычно больше спален. Это может затруднить определение индивидуального влияния отдельных переменных на цены на жилье, что приведет к ненадежным результатам.
Предполагая постоянный разброс ошибок
Линейная регрессия предполагает, что различия между наблюдаемыми и прогнозируемыми значениями (разброс ошибок) одинаковы для всех независимых переменных. Если это не так, прогнозы, сгенерированные моделью, могут быть ненадежными. В контролируемом машинном обучении неспособность учесть разброс ошибок может привести к тому, что модель будет генерировать смещенные и неэффективные оценки, что снижает ее общую эффективность.
