Случайные леса в машинном обучении: какие они есть и как они работают

Случайные леса являются мощной и универсальной техникой в ​​машинном обучении (ML). Это руководство поможет вам понять случайные леса, как они работают, а также их приложения, преимущества и проблемы.

Оглавление

• Что такое случайный лес?
• Деревья решений против случайного леса: в чем разница?
• Как работают случайные леса
• Практическое применение случайных лесов
• Преимущества случайных лесов
• Недостатки случайных лесов

Что такое случайный лес?

Случайный лес - это алгоритм машинного обучения, который использует несколько деревьев решений для прогнозирования. Это контролируемый метод обучения, предназначенный для задач классификации и регрессии. Сочетая выходы многих деревьев, случайный лес повышает точность, снижает переосмысление и обеспечивает более стабильные прогнозы по сравнению с одним деревом решений.

Деревья решений против случайного леса: в чем разница?

Хотя случайные леса построены на деревьях решений, два алгоритма значительно различаются по структуре и применению:

Деревья решений

Дерево решений состоит из трех основных компонентов: корневого узла, узлов принятия решений (внутренних узлов) и листовых узлов. Как блок -схема, процесс принятия решения начинается в корневом узле, протекает через узлы принятия решений на основе условий и заканчивается на листовом узле, представляющем результат. В то время как деревья решений легко интерпретировать и концептуализировать, они также склонны к переоснащению, особенно с сложными или шумными наборами данных.

Случайные леса

Случайный лес - это ансамбль деревьев решений, который сочетает в себе их результаты для улучшения прогнозов. Каждое дерево обусловлено уникальным образцом начальной загрузки (случайно отобранное подмножество исходного набора данных с заменой) и оценивает разделения решений с использованием случайно выбранного подмножества функций в каждом узле. Этот подход, известный как фантастические пакеты, вводит разнообразие среди деревьев. Объединяя прогнозы - использование большинства голосования за классификацию или средние значения для регрессии - Random Forests дают более точные и стабильные результаты, чем любое отдельное дерево решений в ансамбле.

Как работают случайные леса

Случайные леса работают, объединяя несколько деревьев решений для создания надежной и точной модели прогнозирования.

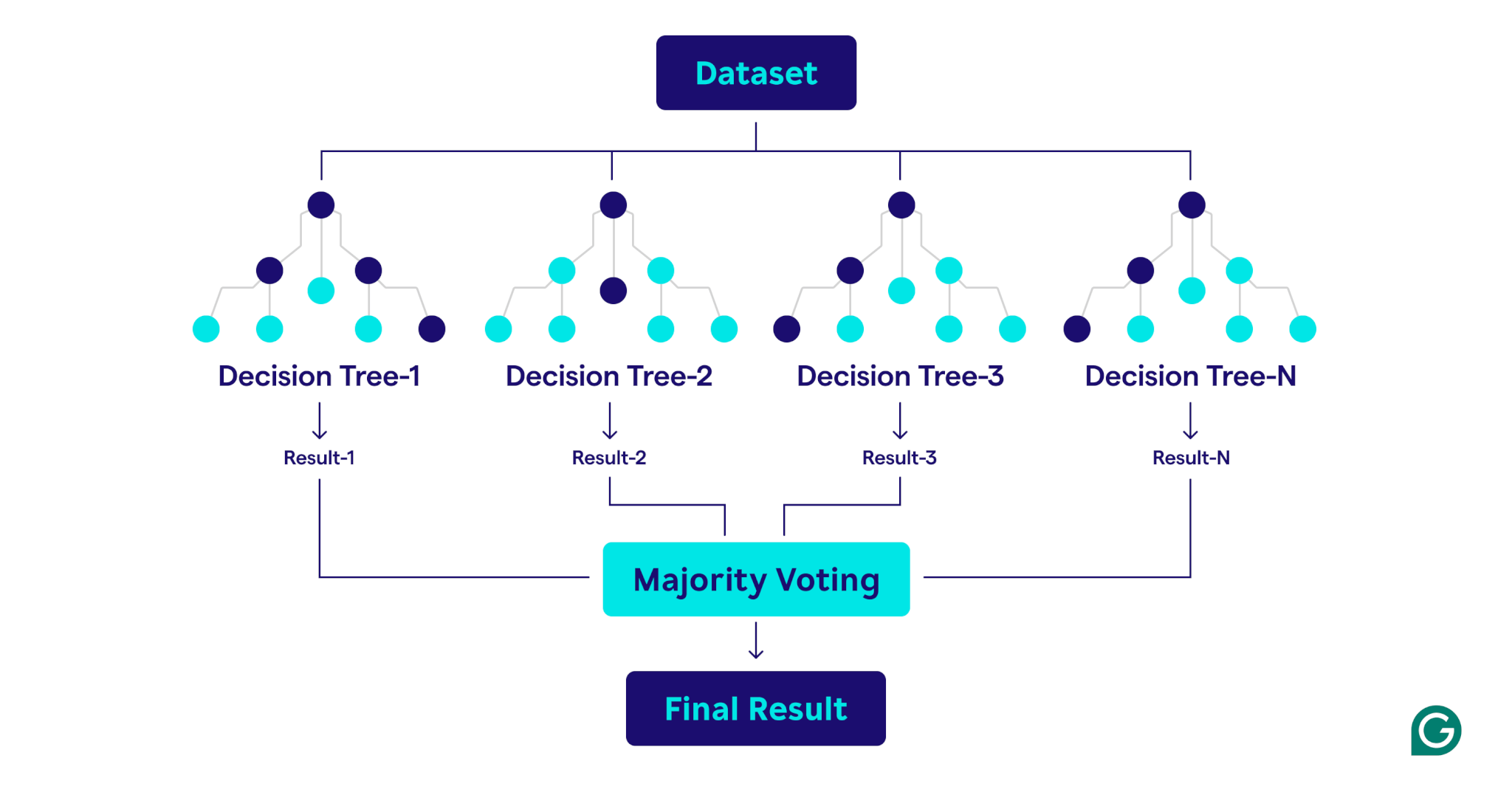
Вот пошаговое объяснение процесса:

1. Установка гиперпараметров

Первым шагом является определение гиперпараметров модели. К ним относятся:

• Количество деревьев:определяет размер леса
• Максимальная глубина для каждого дерева:контролирует, насколько глубоко может расти каждое дерево решений
• Количество функций, рассмотренных при каждом разделении:ограничивает количество функций, оцениваемых при создании разделения

Эти гиперпараметры позволяют тонко настраивать сложность модели и оптимизировать производительность для конкретных наборов данных.

2. Отборка начальной загрузки

Как только гиперпараметры будут установлены, процесс обучения начинается с выборки начальной загрузки. Это включает в себя:

• Точки данных из исходного набора данных выбираются случайным образом для создания обучающих наборов данных (образцов начальной загрузки) для каждого дерева решений.
• Каждый образец начальной загрузки, как правило, примерно в две трети размера исходного набора данных, причем некоторые точки данных повторяются, а другие исключены.
• Оставшаяся треть точек данных, не включенная в образец начальной загрузки, называется данными вне упаковки (OOB).

3. Строительные деревья решений

Каждое дерево решений в случайном лесу обучается на соответствующей образе начальной загрузки, используя уникальный процесс:

• Функция мешков:при каждом разделении выбирается случайная подмножество функций, обеспечивающих разнообразие между деревьями.
• Разделение узлов:лучшая функция из подмножества используется для разделения узла:
  • Для классификационных задач критерии, такие как Джини -Адмер (мера того, как часто случайно выбранного элемента был бы неправильно классифицирован, если он был случайным образом помечен в соответствии с распределением меток класса в узле), измеряют, насколько хорошо разделение разделяет классы.
  • Для задач регрессии такие методы, как снижение дисперсии (метод, который измеряет, насколько разделение узла уменьшает дисперсию целевых значений, что приводит к более точным прогнозам), оценивает, насколько раскол уменьшает ошибку прогнозирования.
• Дерево растет рекурсивно до тех пор, пока оно не будет соответствовать условиям остановки, такими как максимальная глубина или минимальное количество точек данных на узел.

4. Оценка производительности

Поскольку каждое дерево построено, производительность модели оценивается с использованием данных OOB:

• Оценка ошибок OOB обеспечивает непредвзятую меру производительности модели, устраняя необходимость в отдельном наборе данных проверки.
• Благодаря агрегированию прогнозов от всех деревьев, случайный лес достигает повышения точности и уменьшает переосмысление по сравнению с отдельными деревьями решений.

Практическое применение случайных лесов

Как и деревья решений, на которых они построены, случайные леса могут применяться к проблемам классификации и регрессии в самых разных секторах, таких как здравоохранение и финансы.

Классификация состояний пациента

В здравоохранении случайные леса используются для классификации состояний пациентов на основе информации, такой как история болезни, демография и результаты испытаний. Например, чтобы предсказать, может ли у пациента развиться конкретное состояние, такое как диабет, каждое дерево решений классифицирует пациента как риск или не на основе соответствующих данных, а случайный лес делает окончательное определение на основе большинства голосов. Этот подход означает, что случайные леса особенно хорошо подходят для сложных, богатых функциями наборов данных, найденных в здравоохранении.

Прогнозирование по умолчанию по умолчанию

Банки и основные финансовые учреждения широко используют случайные леса для определения права на ссуду и лучше понять риск. Модель использует такие факторы, как доход и кредитный рейтинг для определения риска. Поскольку риск измеряется как непрерывное числовое значение, случайный лес выполняет регрессию вместо классификации. Каждое дерево решений, обученное немного разным образцам начальной загрузки, выводит прогнозируемый показатель риска. Затем случайный лес в среднем усредняет все отдельные прогнозы, что приводит к надежной, целостной оценке риска.

Прогнозирование потери клиента

В маркетинге случайные леса часто используются для прогнозирования вероятности того, что клиент прекратит использование продукта или услуги. Это включает анализ моделей поведения клиентов, таких как частота покупки и взаимодействие с обслуживанием клиентов. Выявляя эти модели, случайные леса могут классифицировать клиентов с риском ухода. С помощью этих пониманий компании могут предпринять проактивные, управляемые данными шаги, чтобы удержать клиентов, такие как предложение программ лояльности или целевые акции.

Прогнозирование цен на недвижимость

Случайные леса могут быть использованы для прогнозирования цен на недвижимость, что является задачей регрессии. Чтобы сделать прогноз, случайный лес использует исторические данные, которые включают такие факторы, как географическое местоположение, квадратные метры и последние продажи в этом районе. Процесс усреднения случайных лесов приводит к более надежному и стабильному прогнозированию цен, чем у отдельного дерева решений, которое полезно на очень нестабильных рынках недвижимости.

Преимущества случайных лесов

Случайные леса предлагают многочисленные преимущества, включая точность, надежность, универсальность и способность оценить важность признаков.

Точность и надежность

Случайные леса являются более точными и надежными, чем отдельные деревья решений. Это достигается путем объединения выходов нескольких деревьев решений, обученных различным образцам начальной загрузки исходного набора данных. Полученное разнообразие означает, что случайные леса менее склонны к переоснащению, чем отдельные деревья решений. Этот ансамблевый подход означает, что случайные леса хороши в обработке шумных данных, даже в сложных наборах данных.

Универсальность

Как и деревья решений, на которых они построены, случайные леса очень универсальны. Они могут выполнять задачи регрессии и классификации, что делает их применимыми к широкому спектру проблем. Случайные леса также хорошо работают с большими, богатыми функциями наборов данных и могут обрабатывать как числовые, так и категориальные данные.

Особенность важности

Случайные леса обладают встроенной способностью оценить важность конкретных особенностей. В рамках процесса обучения случайные леса выводят оценку, которая измеряет, насколько изменяется точность модели, если определенная функция удаляется. Средняя оценки для каждой функции, случайные леса могут обеспечить количественную оценку важности признака. Затем могут быть удалены менее важные особенности, чтобы создать более эффективные деревья и леса.

Недостатки случайных лесов

В то время как случайные леса предлагают много преимуществ, их труднее интерпретировать и дороже обучать, чем одно дерево решений, и они могут выводить прогнозы медленнее, чем другие модели.

Сложность

В то время как случайные леса и деревья решений имеют много общего, случайные леса труднее интерпретировать и визуализировать. Эта сложность возникает потому, что случайные леса используют сотни или тысячи деревьев решений. Природа «Черного ящика» случайных лесов является серьезным недостатком, когда объясняемость модели является требованием.

Вычислительная стоимость

Обучение сотням или тысячам деревьев решений требует гораздо большей мощности обработки и памяти, чем обучение одному дереву решений. Когда задействованы большие наборы данных, вычислительные затраты могут быть еще выше. Это крупное требование к ресурсам может привести к более высокой денежной стоимости и более длительному времени обучения. В результате случайные леса могут быть не практичными в сценариях, таких как Edge Computing, где как вычисления, так и память мало. Однако случайные леса могут быть параллелизированы, что может помочь снизить стоимость вычисления.

Более медленное время прогноза

Процесс прогнозирования случайного леса включает в себя переселение каждого дерева в лесу и агрегирование их результатов, что по своей природе медленнее, чем использование одной модели. Этот процесс может привести к более медленному времени прогнозирования, чем более простые модели, такие как логистическая регрессия или нейронные сети, особенно для крупных лесов, содержащих глубокие деревья. Для вариантов использования, когда время имеет значение, такую ​​как высокочастотная торговля или автономные транспортные средства, эта задержка может быть непомерно высокой.