什麼是機器學習中的線性迴歸?
已發表: 2024-09-06線性迴歸是資料分析和機器學習 (ML) 的基礎技術。本指南將幫助您了解線性迴歸、其建構方式及其類型、應用、優點和缺點。
目錄
- 什麼是線性迴歸?
- 線性迴歸的類型
- 線性迴歸與邏輯迴歸
- 線性迴歸如何運作?
- 線性迴歸的應用
- 機器學習中線性迴歸的優點
- 機器學習中線性迴歸的缺點
什麼是線性迴歸?
線性迴歸是機器學習中使用的統計方法,用於對因變數與一個或多個自變數之間的關係進行建模。它透過將線性方程式擬合到觀測資料來建模關係,通常作為更複雜演算法的起點,並廣泛用於預測分析。
本質上,線性迴歸透過透過一組資料點找到最擬合的直線來對因變數(您想要預測的結果)和一個或多個自變數(您用於預測的輸入特徵)之間的關係進行建模。這條線稱為迴歸線,表示因變數(我們想要預測的結果)和自變數(我們用於預測的輸入特徵)之間的關係。簡單線性迴歸線的方程式定義為:
y = mx + c
其中y是因變量, x是自變量,m 是直線的斜率, c是 y 截距。該方程式提供了一個將輸入映射到預測輸出的數學模型,其目標是最小化預測值和觀測值之間的差異(稱為殘差)。透過最小化這些殘差,線性迴歸產生最能代表資料的模型。
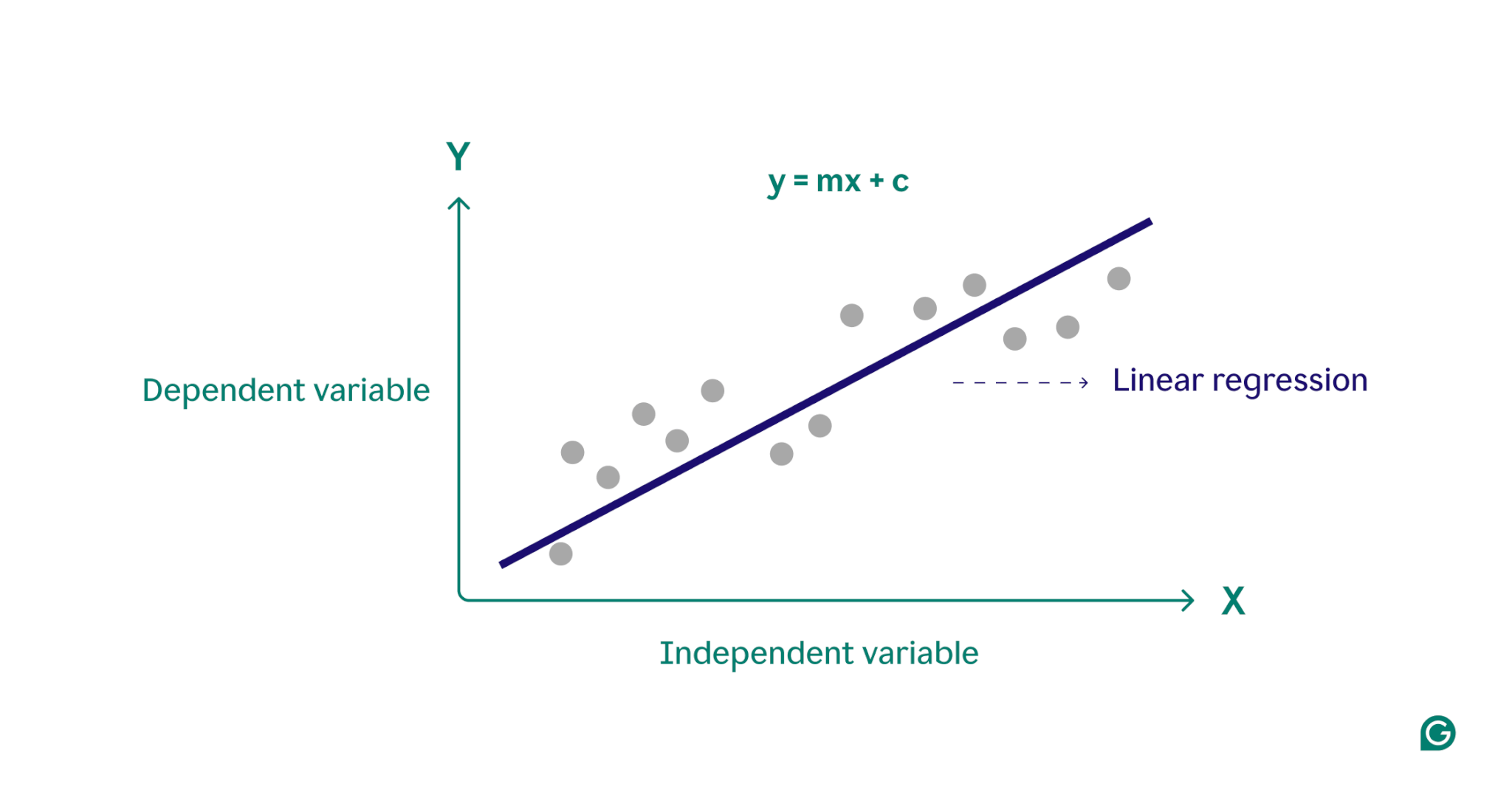
從概念上講,線性迴歸可以視覺化為通過圖表上的點繪製一條直線,以確定這些資料點之間是否存在關係。一組資料點的理想線性迴歸模型是最接近資料集中每個點的值的線。
線性迴歸的類型
線性迴歸主要有兩種類型:簡單線性迴歸和多元線性迴歸。
簡單線性迴歸
簡單線性迴歸使用直線對單一自變數和因變數之間的關係進行建模。簡單線性迴歸的方程式為:
y = mx + c
其中y是因變量, x是自變量, m是直線的斜率, c是 y 截距。
這種方法是在處理單變量場景時獲得清晰見解的直接方法。假設一位醫生試圖了解患者身高如何影響體重。透過在圖表上繪製每個變數並使用簡單線性迴歸找到最佳擬合線,醫生可以僅根據患者的身高來預測患者的體重。
多元線性迴歸
多元線性迴歸擴展了簡單線性迴歸的概念,以適應多個變量,從而可以分析多個因素如何影響因變量。多元線性迴歸方程式為:
y = b 0 + b 1 x 1 + b 2 x 2 + … + b n x n
其中y是因變量, x 1 , x 2 , …, x n是自變量, b 1 , b 2 , …, b n是描述每個自變量與因變量之間關係的係數。
舉個例子,考慮一位想要估算房價的房地產經紀人。代理商可以使用基於單一變數(例如房屋大小或郵遞區號)的簡單線性迴歸,但這種模型過於簡單化,因為房價通常是由多種因素的複雜交互作用所驅動的。多元線性迴歸結合了房屋大小、社區和臥室數量等變量,可能會提供更準確的預測模型。
線性迴歸與邏輯迴歸
線性迴歸經常與邏輯迴歸混淆。雖然線性迴歸預測連續變數的結果,但當因變數是分類變數(通常是二元變數)(是或否)時,使用邏輯迴歸。類別變數定義具有有限數量類別的非數字組,例如年齡組或付款方式。另一方面,連續變數可以取任何數值並且是可測量的。連續變數的範例包括重量、價格和每日溫度。
與線性迴歸中使用的線性函數不同,邏輯迴歸使用稱為邏輯函數的 S 形曲線對分類結果的機率進行建模。在二元分類的範例中,屬於「是」類別的資料點落在 S 形的一側,而屬於「否」類別的資料點落在另一側。實際上,邏輯迴歸可以用來分類電子郵件是否是垃圾郵件,或是預測客戶是否會購買產品。本質上,線性迴歸用於預測定量值,而邏輯迴歸用於分類任務。

線性迴歸如何運作?
線性迴歸的工作原理是透過一組資料點找到最佳擬合線。這個過程涉及:
1選擇模型:第一步,選擇合適的線性方程式來描述因變數和自變數之間的關係。
2擬合模型:接下來,使用一種稱為普通最小二乘法 (OLS) 的技術來最小化觀測值與模型預測值之間的平方差總和。這是透過調整線的斜率和截距來找到最佳擬合來完成的。此方法的目的是最小化預測值與實際值之間的誤差或差異。這個擬合過程是監督機器學習的核心部分,其中模型從訓練資料中學習。
3評估模型:在最後一步中,使用 R 平方等指標評估擬合質量,該指標測量可從自變量預測的因變量中的方差比例。換句話說,R 平方衡量資料與迴歸模型的實際適合度。
線性迴歸在機器學習的應用
在機器學習中,線性迴歸是預測結果和理解各領域變數之間關係的常用工具。以下是其應用的一些著名範例:
預測消費者支出
收入水準可用於線性迴歸模型來預測消費者支出。具體來說,多元線性迴歸可以結合歷史收入、年齡和就業狀況等因素來提供全面的分析。這可以幫助經濟學家製定數據驅動的經濟政策,並幫助企業更了解消費者的行為模式。
分析行銷影響
行銷人員可以使用線性迴歸來了解廣告支出如何影響銷售收入。透過對歷史數據應用線性迴歸模型,可以預測未來的銷售收入,從而使行銷人員能夠優化其預算和廣告策略以獲得最大影響。
預測股票價格
在金融界,線性迴歸是用來預測股票價格的眾多方法之一。利用歷史股票數據和各種經濟指標,分析師和投資者可以建立多個線性迴歸模型,幫助他們做出更明智的投資決策。
預測環境條件
在環境科學中,線性迴歸可用於預測環境條件。例如,交通量、天氣狀況和人口密度等各種因素可以幫助預測污染物水平。然後,政策制定者、科學家和其他利害關係人可以使用這些機器學習模型來了解和減輕各種行為對環境的影響。
機器學習中線性迴歸的優點
線性迴歸具有多種優勢,使其成為機器學習中的關鍵技術。
易於使用和實施
與大多數數學工具和模型相比,線性迴歸易於理解和應用。對於新的機器學習從業者來說,它尤其適合作為起點,提供寶貴的見解和經驗,作為更高級演算法的基礎。
計算效率高
機器學習模型可能是資源密集的。與許多演算法相比,線性迴歸需要相對較低的運算能力,但仍可提供有意義的預測見解。
可解釋的結果
先進的統計模型雖然強大,但通常難以解釋。使用線性迴歸這樣的簡單模型,變數之間的關係很容易理解,每個變數的影響可以透過其係數清楚地表明。
先進技術基礎
理解和實現線性迴歸為探索更先進的機器學習方法奠定了堅實的基礎。例如,多項式迴歸建立在線性迴歸的基礎上,用於描述變數之間更複雜的非線性關係。
機器學習中線性迴歸的缺點
雖然線性迴歸是機器學習中的一個有價值的工具,但它有幾個明顯的限制。了解這些缺點對於選擇合適的機器學習工具至關重要。
假設線性關係
線性迴歸模型假設因變數和自變數之間的關係是線性的。在複雜的現實場景中,情況可能並不總是如此。例如,一個人一生中的身高是非線性的,童年時期的快速增長會在成年後減慢並停止。因此,使用線性迴歸預測身高可能會導致預測不準確。
對異常值的敏感度
離群值是顯著偏離資料集中大多數觀測值的資料點。如果處理不當,這些極值點可能會扭曲結果,導致結論不準確。在機器學習中,這種敏感度意味著異常值可能會嚴重影響模型的預測準確性和可靠性。
多重共線性
在多元線性迴歸模型中,高度相關的自變數可能會扭曲結果,這種現象稱為多重共線性。例如,房屋中的臥室數量與其大小可能高度相關,因為較大的房屋往往有更多的臥室。這可能會導致很難確定單一變數對房價的影響,從而導致結果不可靠。
假設誤差分佈恆定
線性迴歸假設所有自變數的觀測值和預測值之間的差異(誤差分佈)相同。如果情況並非如此,則模型產生的預測可能不可靠。在監督機器學習中,未能解決誤差擴散問題可能會導致模型產生偏差且低效的估計,從而降低其整體有效性。
